题目内容
已知点(1, )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
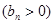 的首项为
的首项为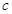 ,且前
,且前 项和
项和 满足
满足 -
- =
= +
+ (
( ).
).
(1)求数列 和
和 的通项公式;
的通项公式;
(2)求数列{ 前
前 项和为
项和为 .
.
【答案】
(1)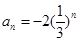 ,
,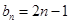 ;(2) 112.
;(2) 112.
【解析】
试题分析:(1)根据已知条件先求出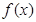 的表达式,这样等比数列
的表达式,这样等比数列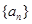 前
前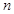 项和
项和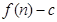 就清楚了,既然数列
就清楚了,既然数列 是等比数列,我们可以用特殊值
是等比数列,我们可以用特殊值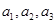 来求出参数
来求出参数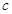 的值,从而求出
的值,从而求出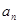 ,对数列
,对数列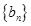 ,由前
,由前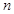 项和
项和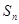 满足
满足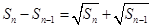 ,可变形为
,可变形为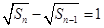 ,即数列
,即数列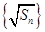 为等差数列,可以先求出
为等差数列,可以先求出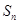 ,再求出
,再求出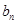 .(2)关键是求出和
.(2)关键是求出和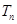 ,而数列{
,而数列{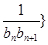 前
前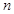 项和
项和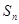 就可用裂项相消法求出,
就可用裂项相消法求出,
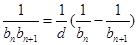 (
(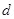 是数列
是数列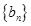 的公差}.
的公差}.
试题解析:(1)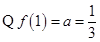 ,
,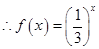
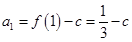 ,
,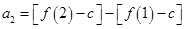
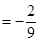 ,
,
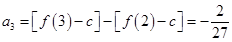 .
.
又数列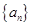 成等比数列,
成等比数列,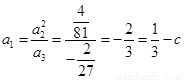 ,所以
,所以
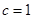 ;
;
又公比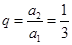 ,所以
,所以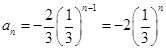
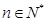 ; 3分
; 3分
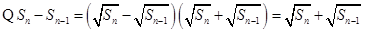
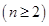
又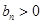 ,
,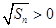 ,
,
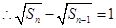 ;
;
数列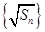 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,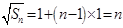 ,
,
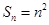
当 ,
,
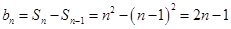 ;
;
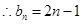 (
(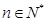 ); 7分
); 7分
(2)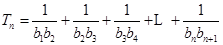
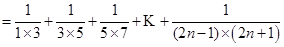

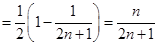 ; 12分
; 12分
考点:(1)①等比数列的定义;②由数列前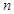 项和
项和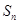 求数列通项;(2)裂项相消法求数列前
求数列通项;(2)裂项相消法求数列前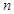 项和.
项和.

练习册系列答案
相关题目
 )是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少? )是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少? )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
 的首项为
的首项为 ,且前
,且前 满足
满足 =
= +
+ (
(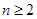 ).
). 前
前 ,问
,问 的最小正整数
的最小正整数