题目内容
如图,过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2).(1)求该抛物线上纵坐标为![]() 的点到其焦点F的距离;?
的点到其焦点F的距离;?
(2)当PA与PB的斜率存在且倾斜角互补时,求![]() 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
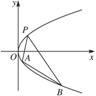
思路分析:(1)抛物线上的点到焦点的距离往往利用抛物线的定义转化成到准线的距离.(2)直线被圆锥曲线所截涉及弦的中点、斜率等问题时,可用方程组的知识处理,也可用“代点平方差”的方法解决,后者较简单.?
解:(1)当y=![]() 时,x=
时,x=![]() .
.
又抛物线y2=2px的准线方程为x=-![]() ,由抛物线定义得
,由抛物线定义得
所求距离为![]() -(-
-(-![]() )=
)=![]() .
.

(2)设直线PA的斜率为kPA,直线PB的斜率kPB.
由y12=2px1,y02=2px0,
相减得(y1-y0)(y1+y0)=2p(x1-x0),?
故kPA=![]() (x1≠x0).
(x1≠x0).
同理可得kPB=![]() (x2≠x0).?
(x2≠x0).?
由PA、PB倾斜角互补知kPA=-kPB,?
即![]() =-
=-![]() ,?
,?
所以y1+y2=-2y0,?
故![]() =-2.?
=-2.?
设直线AB的斜率为kAB.?
由y22=2px2,y12=2px1,?
相减得(y2-y1)(y2+y1)=2p(x2-x1),?
所以kAB=![]() (x1≠x2).
(x1≠x2).
将y1+y2=-2y0(y0>0)代入得?
kAB=![]() ,所以kAB是非零常数.
,所以kAB是非零常数.
思维启示:直线被圆锥曲线所截时,用“代点平方差”,可得到x1+x2,y1+y2,x1-x2,y1-y2的等量关系式,故可解决与弦的中点、直线的斜率有关的问题,但这种方法不能保证直线是否存在,应注意验证.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
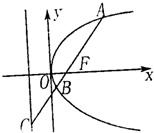 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|=
78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|= 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为 如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( )
如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( ) 如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则
如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则