题目内容
 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为y2=2x
y2=2x
.分析:设A(x1,y1),B(x2,y2),由抛物线的定义得到x1=2-
,再由|BC|=2|BF|解出x2=
,利用抛物线的性质x1x2=
建立关于p的方程,解之可得p=1,即得此抛物线的方程.
| p |
| 2 |
| p |
| 6 |
| p2 |
| 4 |
解答:解:设A(x1,y1),B(x2,y2)
由抛物线的定义,得|AF|=
+x1=2,
∴x1=2-
∵直线l交抛物线准线于点C,|BC|=2|BF|,
∴x2=
,
由抛物线的性质,得x1x2=
(2-
)=
解之得p=1,可得此抛物线的方程为y2=2x
故答案为:y2=2x
由抛物线的定义,得|AF|=
| p |
| 2 |
∴x1=2-
| p |
| 2 |
∵直线l交抛物线准线于点C,|BC|=2|BF|,
∴x2=
| p |
| 6 |
由抛物线的性质,得x1x2=
| p |
| 6 |
| p |
| 2 |
| p2 |
| 4 |
解之得p=1,可得此抛物线的方程为y2=2x
故答案为:y2=2x
点评:本题给出抛物线满足的条件,求抛物线的方程.着重考查了抛物线的定义与标准方程、直线与圆锥曲线位置关系等知识,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
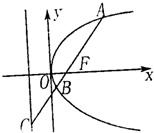 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|=
78、如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|•|CD|= 如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( )
如图,过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l交抛物线于A、B两点,若|AF|=3,则此抛物线方程为( ) 如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则
如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则