题目内容
(13分)已知圆 和直线
和直线 .
.
⑴ 证明:不论 取何值,直线
取何值,直线 和圆
和圆 总相交;
总相交;
⑵ 当 取何值时,圆
取何值时,圆 被直线
被直线 截得的弦长最短?并求最短的弦的长度.
截得的弦长最短?并求最短的弦的长度.
 和直线
和直线 .
.⑴ 证明:不论
 取何值,直线
取何值,直线 和圆
和圆 总相交;
总相交;⑵ 当
 取何值时,圆
取何值时,圆 被直线
被直线 截得的弦长最短?并求最短的弦的长度.
截得的弦长最短?并求最短的弦的长度.24.⑴. 【证明】
方法一:圆 的方程可化为:
的方程可化为: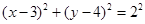 ,圆心为
,圆心为 ,半径
,半径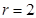 .
.
直线 的方程可化为:
的方程可化为: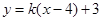 ,直线过定点
,直线过定点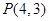 ,斜率为
,斜率为 .
.
定点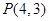 到圆心
到圆心 的距离
的距离 ,
,
∴定点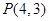 在圆
在圆 内部,∴不论
内部,∴不论 取何值,直线
取何值,直线 和圆
和圆 总相交.
总相交.
方法二:圆 的方程可化为:
的方程可化为: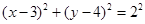 ,圆心为
,圆心为 ,半径
,半径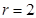 .
.
圆心 到直线
到直线 的距离
的距离 ,
,
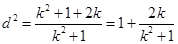 ,因
,因 ,
,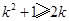 ,
, ,
,
故 ,∴不论
,∴不论 取何值,直线
取何值,直线 和圆
和圆 总相交.
总相交.
⑵. 圆心 到直线
到直线 的距离
的距离
 被直线
被直线 截得的弦长=
截得的弦长=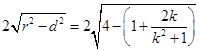 ,
,
当 时,弦长
时,弦长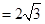 ;
;
当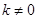 时,弦长
时,弦长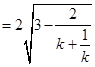 ,下面考虑先求函数
,下面考虑先求函数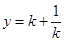 的值域.
的值域.
由函数知识可以证明:函数在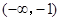 上单调递增,在
上单调递增,在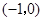 上单调递减,在
上单调递减,在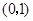 上单调递减,在
上单调递减,在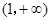 上单调递增(证明略),
上单调递增(证明略),
故当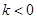 时,函数在
时,函数在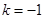 处取得最大值-2;当
处取得最大值-2;当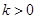 时,函数在
时,函数在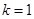 处取得最小值2.
处取得最小值2.
即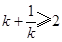 或
或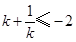 ,
,
故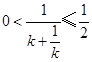 或
或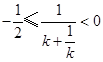 ,可得
,可得
 或
或 ,即
,即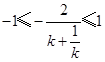 且
且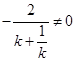 ,
,
 且
且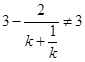 ,
,
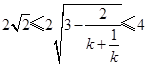 且
且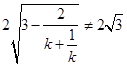 .
.
综上,当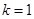 时,弦长取得最小值
时,弦长取得最小值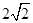 ;当
;当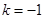 时,弦长取得最大值4.
时,弦长取得最大值4.
方法一:圆
 的方程可化为:
的方程可化为: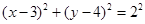 ,圆心为
,圆心为 ,半径
,半径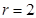 .
.直线
 的方程可化为:
的方程可化为: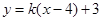 ,直线过定点
,直线过定点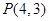 ,斜率为
,斜率为 .
.定点
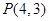 到圆心
到圆心 的距离
的距离 ,
,∴定点
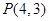 在圆
在圆 内部,∴不论
内部,∴不论 取何值,直线
取何值,直线 和圆
和圆 总相交.
总相交.方法二:圆
 的方程可化为:
的方程可化为: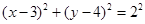 ,圆心为
,圆心为 ,半径
,半径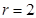 .
.圆心
 到直线
到直线 的距离
的距离 ,
,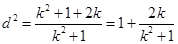 ,因
,因 ,
,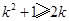 ,
, ,
,故
 ,∴不论
,∴不论 取何值,直线
取何值,直线 和圆
和圆 总相交.
总相交.⑵. 圆心
 到直线
到直线 的距离
的距离
 被直线
被直线 截得的弦长=
截得的弦长=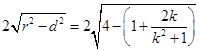 ,
,当
 时,弦长
时,弦长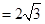 ;
;当
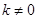 时,弦长
时,弦长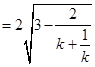 ,下面考虑先求函数
,下面考虑先求函数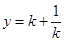 的值域.
的值域.由函数知识可以证明:函数在
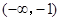 上单调递增,在
上单调递增,在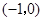 上单调递减,在
上单调递减,在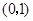 上单调递减,在
上单调递减,在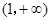 上单调递增(证明略),
上单调递增(证明略),故当
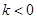 时,函数在
时,函数在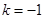 处取得最大值-2;当
处取得最大值-2;当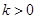 时,函数在
时,函数在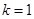 处取得最小值2.
处取得最小值2.即
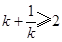 或
或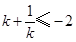 ,
,故
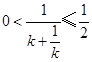 或
或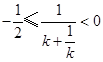 ,可得
,可得 或
或 ,即
,即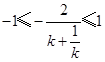 且
且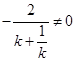 ,
, 且
且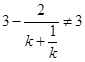 ,
,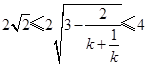 且
且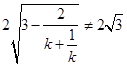 .
.综上,当
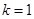 时,弦长取得最小值
时,弦长取得最小值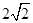 ;当
;当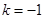 时,弦长取得最大值4.
时,弦长取得最大值4.略

练习册系列答案
相关题目
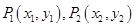 间的“L-距离”定义为
间的“L-距离”定义为 则平面内与
则平面内与 轴上两个不同的定点
轴上两个不同的定点 的“L-距离”之和等于定值(大于
的“L-距离”之和等于定值(大于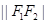 )的点的轨迹可以是( )
)的点的轨迹可以是( )
 的焦点为
的焦点为 ,抛物线
,抛物线 与椭圆在第一象限的交点为
与椭圆在第一象限的交点为 ,若
,若 。
。 的面积;
的面积;  ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线 与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点. =0,求直线PQ的方程.
=0,求直线PQ的方程. 的方程
的方程 ,直线
,直线

 的取值范围; (2)若圆
的取值范围; (2)若圆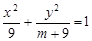 的离心率是
的离心率是 ,则
,则 的值等于
的值等于  程为________.
程为________.