题目内容
已知平面向量
,
(
≠
,
≠0)满足|
|=1,(1)当|
-
|=|
+
|=2时,求|
|的值;(2)当
与
-
的夹角为120°时,求|
|的取值范围.
| α |
| β |
| α |
| β |
| β |
| α |
| α |
| β |
| α |
| β |
| β |
| β |
| α |
| β |
| β |
(1)|
-
|=|
+
|=2即|
-
|2=|
+
|2=4,化简得
∵|
|=1,∴|
|=
,即|
|的值为
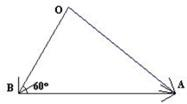
(2)如图,设
=
,
=
,∴
=
-
,
由题,
与
-
的夹角为120°,因此,在△ABO中,∠OBA=60°,根据正弦定理,
=
,
∴|
|=
sinA,∵0°<A<120°∴0<sinA≤1,
即|
|的取值范围是(0,
].
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| β |
|
∵|
| α |
| β |
| 3 |
| β |
| 3 |
(2)如图,设
| OA |
| α |
| OB |
| β |
| BA |
| α |
| β |
由题,
| β |
| α |
| β |
|
| ||
| sinA |
|
| ||
| sinB |
∴|
| β |
2
| ||
| 3 |
即|
| β |
2
| ||
| 3 |


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 和直线
和直线 .
. 取何值,直线
取何值,直线 和圆
和圆 总相交;
总相交; 的顶点
的顶点 ,
,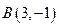 ,
, 求顶点
求顶点 的坐标.
的坐标.