题目内容
已知△ABC的三个内角A、B、C的对边分别为a、b、c，若a、b、c成等差数列，且2cos2B-8cosB+5=0，求角B的大小，并判断△ABC的形状。
解：∵2cos2B-8cosB+5=0，
∴2（2cos2B-1）-8cosB+5=0
∴4cos2B-8cosB+3=0，
即（2cosB-1）（2cosB-3）=0
解得cosB=
或cosB=
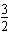（舍去）
∵0＜B＜π，
∴B=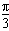
∵a，b，c成等差数列，
∴a+c=2b
∴cosB=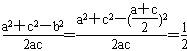
化简得a2+c2-2ac=0，解得a=c
∴△ABC是等边三角形。
∴2（2cos2B-1）-8cosB+5=0
∴4cos2B-8cosB+3=0，
即（2cosB-1）（2cosB-3）=0
解得cosB=
或cosB=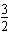（舍去）∵0＜B＜π，
∴B=
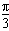
∵a，b，c成等差数列，
∴a+c=2b
∴cosB=
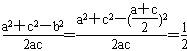
化简得a2+c2-2ac=0，解得a=c
∴△ABC是等边三角形。
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目