题目内容
 已知抛物线
已知抛物线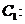
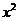 =
=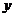 ,圆
,圆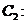
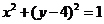 的圆心为点M。
的圆心为点M。
(Ⅰ)求点M到抛物线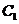 的准线的距离;
的准线的距离;
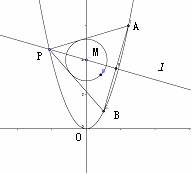
(Ⅱ)已知点P是抛物线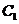 上一点(异于原点),过点P作圆
上一点(异于原点),过点P作圆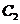 的两条切线,交抛物线
的两条切线,交抛物线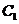 于A,B两点,若过M,P两点的直线
于A,B两点,若过M,P两点的直线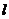 垂足于AB,求直线
垂足于AB,求直线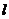 的方程.
的方程.
【答案】
本题考查抛物线的几何性质,直线与抛物线,圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力。满分15分。
(Ⅰ)解:由题意可知,抛物线的准线方程为: 所以圆心M(0,4)到抛物线的距离是
所以圆心M(0,4)到抛物线的距离是
 (Ⅱ)解:设P(x0, x02),A(
(Ⅱ)解:设P(x0, x02),A( )B(
)B( ),由题意得
),由题意得 设过点P的圆C2的切线方程为y-x0=k(x- x0)
设过点P的圆C2的切线方程为y-x0=k(x- x0)
即 , ①
, ①
则
即
设PA,PB的斜率为 ,则
,则 是上述方程的两根,所以
是上述方程的两根,所以
 ,
,
将①代入 得
得 ,
,
由于 是此方程的根,故
是此方程的根,故 所以
所以


由MP⊥AB,得 ,解得
,解得
即点P的坐标为 ,所以直线l的方程为
,所以直线l的方程为 。
。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
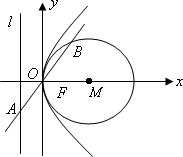
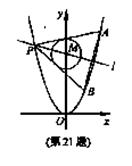
 的最小值;
的最小值;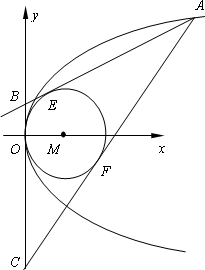
 (Ⅱ)已知点P是抛物线
(Ⅱ)已知点P是抛物线