Question

已知抛物线y²＝2px(p＞0)上一个横坐标为2的点到其焦点的距离为．

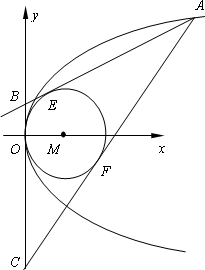
(1)求p的值；

(2)若A是抛物线y²＝2px上的一动点，过A作圆M：(x－1)²＋y²＝1的两条切线分别切圆于E、F两点，交y轴于B、C两点，当A点横坐标大于2时，求△ABC的面积的最小值．

Answer 1

答案：
解析：

解：(1)由抛物线的定义知，， 　　所以　　4分 　　(2)设A(x0，y0)，B(0，b)，C(0，c)， 　　直线AB的方程为y－b＝， 　　即(y0－b)x－x0y＋x0b＝0 　　又圆心(1，0)到AB的距离为1，所以＝1　　7分 　　即(y0－b)2＋x＝(y0－b)2＋2x0b(y0－b)＋xb2 　　又x0＞2，上式化简得(x0－2)b2＋2y0b－x0＝0　　9分 　　同理有(x0－2)c2＋2y0c－x0＝0 　　故b，c是方程(x0－2)t2＋2y0t－x0＝0的两个实数根 　　所以b＋c＝，bc＝　　11分 　　则(b－c)2＝＝， 　　即|b－c|＝， 　　∴S△ABC＝|b－c|x0＝＝x0－2＋＋4≥2＋4＝8　　13分 　　当(x0－2)2＝4时，上式取等号，此时x0＝4，y＝±2 　　因此S△ABC的最小值为8　　15分