题目内容
已知
，函数
（
的图像连续不断）
（Ⅰ）求的单调区间；
（Ⅱ）当
时，证明：存在
，使
；
（Ⅲ）若存在均属于区间
的
，且
，使
，证明
．
本小题主要考查导数的运算、利用导数研究函数的单调性、解不等式、函数的零点等基础知识，考查运算能力和运用函数思想分析解决问题的能力及分类讨论的思想方法.满分14分.
（I）解：
，
令
当x变化时，
的变化情况如下表：
|
|
|
|
|
|
| + | 0 | - |
|
|
| 极大值 |
|
所以，的单调递增区间是
的单调递减区间是
（II）证明：当
由（I）知在（0，2）内单调递增，
在
内单调递减.
令
由于在（0，2）内单调递增，
故
取
所以存在
即存在
（说明：
的取法不唯一，只要满足
即可）
（III）证明：由及（I）的结论知
，
从而
上的最小值为
又由，
知
故
从而
练习册系列答案
阅读快车系列答案
相关题目
．
时，求函数
的极值；w.w.w.k.s.5.u.c.o.m 
；
处的切线的斜率为
，求证：
是
成立的充要条件． 
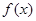满足：①在x=1时有极值；②图像过点
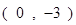，且在该点处的切线与直线
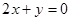平行.
的值域；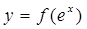
上任意两点的连线的斜率恒大于
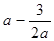，求
的取值范围.
，数列
的通项公式是
，前
项和记作
(
1，2，…），规定
．函数
在
处和每个区间
（
0，1，2，…）上有定义，且
，
（
时，
（
，
）与点
（
，
）的线段上．
:
（
, 求
;
，求
的取值范围．
的图象上任意不同的两点的连线的斜率小于1，
的图像上的任意一点的切线的斜率为k，
成立的充要条件。
的图象上任意不同的两点的连线的斜率小于1，求证：
的图像上的任意一点的切线的斜率为k，
成立的充要条件。