题目内容
已知
=(1,2+sinx),
=(2,cosx),
=(-1,2),(
-
)∥
,则锐角x等于( )
| a |
| b |
| c |
| a |
| c |
| b |
分析:先求出得
-
的坐标,再由(
-
)∥
求得 tanx=1,由此求得锐角x的值.
| a |
| c |
| a |
| c |
| c |
解答:解:由题意可得
-
=(-1,2+sinx-cosx),再由(
-
)∥
可得-2-(-1)(2+sinx-cosx)=0,
化简可得 sinx=cosx,
∴tanx=1,
∴锐角x等于45°,
故选C.
| a |
| c |
| a |
| c |
| c |
化简可得 sinx=cosx,
∴tanx=1,
∴锐角x等于45°,
故选C.
点评:本题主要考查两个向量共线的性质,两个向量坐标形式的运算,同角三角函数的基本关系的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
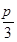 ,S△ABC=6
,S△ABC=6