题目内容
9.在△ABC中,a=4,b=2$\sqrt{2}$,∠A=45°,则∠B=30°.分析 由正弦定理,解得sinB.再由b<a,可得B<A=45°,由此可得B的值.
解答 解:在△ABC中,∠A=45°,a=4,b=2$\sqrt{2}$,则由正弦定理可得$\frac{4}{sin45°}=\frac{2\sqrt{2}}{sinB}$,解得sinB=$\frac{1}{2}$.
再由b<a,可得B<A,故B为锐角,故B=30°,
故答案为:30°.
点评 本题主要考查正弦定理的应用,大边对大角,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
17.已知A={x|-1<x<2},B={x|x≤1},则A∩(∁RB)=( )
| A. | {x|1<x<2} | B. | {x|-1<x<1} | C. | {x|-1<x<2} | D. | {x|1≤x<2} |
4.函数y=$\sqrt{{x}^{2}-2x-3}$的定义域为( )
| A. | [-1,3] | B. | (-∞,-1)∪(3,+∞) | C. | (-1,3) | D. | (-∞,-1]∪[3,+∞) |
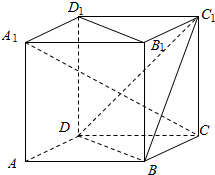 如图,ABCD-A1B1C1D1是棱长为1正方体.
如图,ABCD-A1B1C1D1是棱长为1正方体.