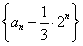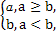题目内容
已知集合A={y|y=x2- x+1,x∈[
x+1,x∈[ ,2]},B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
,2]},B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
(-∞,- ]∪[
]∪[ ,+∞)
,+∞)
【解析】y=x2- x+1=(x-
x+1=(x- )2+
)2+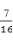 ,
,
∵x∈[ ,2],∴
,2],∴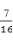 ≤y≤2,
≤y≤2,
∴A={y|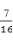 ≤y≤2}.
≤y≤2}.
由x+m2≥1,得x≥1-m2,
∴B={x|x≥1-m2}.
∵“x∈A”是“x∈B”的充分条件,∴A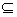 B,
B,
∴1-m2≤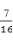 ,解得m≥
,解得m≥ 或m≤-
或m≤- ,
,
故实数m的取值范围是(-∞,- ]∪[
]∪[ ,+∞).
,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目