题目内容
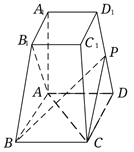
【题目】如图，在正方体
中，
是
的中点．
(1)求证：
平面
；
(2)求异面直线
和
所成角的大小．
【答案】（1）证明见解析；（2）
.
【解析】
（1）连接
交
于点
，连接
，结合三角形中位线定理，及线面平行的判定定理，可得
平面
；(2)由
，知
和所成的角等于和所成的角，根据等边三角形的性质可得结论.
(1)证明：如图，连接D1C交DC1于点O1，连接OO1，
∵O、O1分别是AC和D1C的中点，
∴OO1∥AD1.
又OO1平面DOC1，AD1平面DOC1，
∴AD1∥平面DOC1.
(2)由OO1∥AD1知，AD1和DC1所成角等于OO1和DC1所成的锐角或直角．设正方体的棱长为1.
在△OO1D中，DO1＝
，DO＝，OO1＝
AD1＝，
∴△OO1D是等边三角形．
∴异面直线AD1与DC1所成的角为60°.
练习册系列答案
阅读快车系列答案
相关题目
【题目】在用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一周期内的图象时，列表并填入了部分数据，如下表：
ωx+φ | 0 |
| π |
| 2π |
x | π |
| |||
Asin（ωx+φ） | 0 | 3 | ﹣3 | 0 |
（1）请将上表空格中处所缺的数据填写在答题卡的相应位置上，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点的横坐标缩短为原来的 
，再将所得图象向左平移 
个单位，得到y=g（x）的图象，求g（x）的单调递增区间．
