题目内容
已知命题p:?x∈R,cosx=;命题q:?x∈R,x2-x+1>0.则下列结论正确的是( )
A.命题 是假命题 是假命题 | B.命题 是真命题 是真命题 |
C.命题 是真命题 是真命题 | D.命题 是真命题 是真命题 |
D
解析试题分析:因为 ,故命题
,故命题 是假命题;因为
是假命题;因为 ,故命题
,故命题 是真命题,故选D.
是真命题,故选D.
考点:复合命题的真假判断.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
“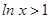 ”是“x>l"的( )
”是“x>l"的( )
| A.充要条件 | B.必要非充分条件 |
| C.充分非必要条件 | D.既不充分也不必要条件 |
已知两个平面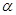 、
、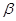 ,直线
,直线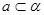 ,则“
,则“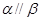 ”是“直线
”是“直线
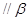 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p:?x∈[0, ],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
A.[- ,-1] ,-1] |
B.[- ,2] ,2] |
| C.[-1,2] |
D.[- ,+∞) ,+∞) |
下面几个命题中,假命题是( )
A.“若 ,则 ,则 ”的否命题; ”的否命题; |
B.“ ,函数 ,函数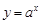 在定义域内单调递增”的否定; 在定义域内单调递增”的否定; |
C.“ 是函数 是函数 的一个周期”或“ 的一个周期”或“ 是函数 是函数 的一个周期”; 的一个周期”; |
D.“ ”是“ ”是“ ”的必要条件. ”的必要条件. |
在一次投掷链球比赛中,甲、乙两位运动员各投掷一次,设命题p是“甲投掷在20米之外”,q是“乙投掷在20米之外”,则命题“至少有一位运动员没有投掷在20米之外”可表示为( )
| A.p或q | B.p或非q | C.非p且非q | D.非p或非q |
“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
“ ”是“
”是“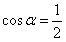 ”的( )
”的( )
| A.必要不充分条件 |
| B.充分不必要条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
命题“若-1<x<1,则x2<1”的逆否命题是( )
| A.若x≥1或x≤-1,则x2≥1 |
| B.若x2<1,则-1<x<1 |
| C.若x2>1,则x>1或x<-1 |
| D.若x2≥1,则x≥1或x≤-1 |