题目内容
已知两个平面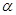 、
、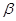 ,直线
,直线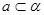 ,则“
,则“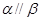 ”是“直线
”是“直线
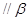 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:由直线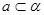 ,则“
,则“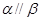 ”是
”是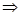 “直线
“直线
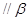 ”成立,因为两平面
”成立,因为两平面 没有公共点,则平面内
没有公共点,则平面内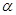 直线
直线 与平面
与平面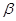 自然没有公共点;反过来,由直线
自然没有公共点;反过来,由直线 与平面
与平面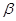 平行,则经过直线
平行,则经过直线 的平面
的平面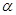 与平面
与平面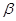 的位置关系是平行或相交,所以“
的位置关系是平行或相交,所以“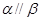 ”是
”是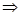 “直线
“直线
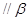 ”不成立;所以“
”不成立;所以“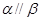 ”是“直线
”是“直线
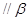 ”的充分不必要条件.
”的充分不必要条件.
考点:1、直线与平面、平面与平面的位置关系;2、命题与充要条件.

练习册系列答案
相关题目
命题:“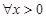 ,都有
,都有 ”的否定是( )
”的否定是( )
A.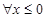 ,都有 ,都有 | B.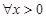 ,都有 ,都有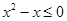 |
C.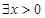 ,使得 ,使得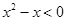 | D.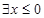 ,使得 ,使得 |
设 在(
在( )上单调递增;
)上单调递增; ,则p是q的( )
,则p是q的( )
| A.充要条件 | B.充分不必要条件 | C.必要不充分条件 | D.以上都不对 |
已知命题p:?x∈R,cosx=;命题q:?x∈R,x2-x+1>0.则下列结论正确的是( )
A.命题 是假命题 是假命题 | B.命题 是真命题 是真命题 |
C.命题 是真命题 是真命题 | D.命题 是真命题 是真命题 |
设 为正实数,则“
为正实数,则“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.既不充分也不必要条件 | D.充要条件 |
钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的 ( )
| A.充分条件 | B.必要条件 |
| C.充分必要条件 | D.既非充分也非必要条件 |
命题“对任意的x∈R,x3﹣x2+1≤0”的否定是( )
| A.不存在x∈R,x3﹣x2+1≤0 | B.存在x∈R,x3﹣x2+1≤0 |
| C.存在x∈R,x3﹣x2+1>0 | D.对任意的x∈R,x3﹣x2+1>0 |
若 且
且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |