题目内容
过定点P(2,1)作直线l,分别与x轴、y轴正向交于A、B两点,求使△AOB面积最小时的直线方程.
解:显然所求直线l的斜率存在且小于0,设其为k(k<0),则l的方程为y-1=k(x-2).
令y=0,得A(2-![]() ,0);
,0);
令x=0,得B(0,1-2k).
∴S△OAB=![]() |OA|·|OB|=
|OA|·|OB|=![]() |2-
|2-![]() |·|1-2k|=
|·|1-2k|=![]() (2-
(2-![]() )·(1-2k)=
)·(1-2k)=![]() (4-
(4-![]() -4k).
-4k).
其中k<0,-![]() -4k≥2
-4k≥2![]() =4,当且仅当-
=4,当且仅当-![]() =-4k,即k=-
=-4k,即k=-![]() 时,-
时,-![]() -4k的最小值为4.此时S△OAB的最小值为
-4k的最小值为4.此时S△OAB的最小值为![]() (4+4)=4.
(4+4)=4.
故所求直线方程为y-1=-![]() (x-2),即x+2y-4=0.
(x-2),即x+2y-4=0.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
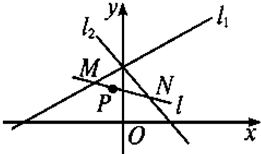 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.