题目内容
过定点P(2,1)作直线l,分别与x轴、y轴正向交于A、B两点,求使△AOB面积最小时的直线方程.
解：显然所求直线l的斜率存在且小于0.设其为k(k＜0),则l的方程为y-1=k(x-2). 令y=0,得A(2- ∴S△OAB= 当且仅当-
,0);令x=0,得B(0,1-2k).
|OA|·|OB|=
|2-
|·|1-2k|=
(2-
)·(1-2k)=
(4-
-4k),其中k＜0,-
-4k≥2
=4.
=-4k,即k=-
时,-
-4k的最小值为4.此时S△OAB的最小值为
(4+4)=4.故所求直线方程为y-1=-
(x-2),即x+2y-4=0.
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
相关题目
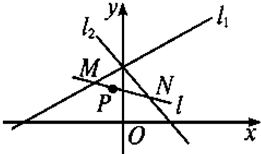如图，已知两条直线l1：x-3y+12=0，l2：3x+y-4=0，过定点P（-1，2）作一条直线l，分别与l1，l2交于M、N两点，若P点恰好是MN的中点，求直线l的方程．