题目内容
2.已知数列{an}的前n项和为Sn,且$\frac{1}{{a}_{n}+1}$=$\frac{3}{{a}_{n+1}+1}$,a2=5,则S6=722.分析 $\frac{1}{{a}_{n}+1}$=$\frac{3}{{a}_{n+1}+1}$,可得an+1+1=3(an+1),利用等比数列的通项公式与求和公式即可得出.
解答 解:∵$\frac{1}{{a}_{n}+1}$=$\frac{3}{{a}_{n+1}+1}$,∴an+1+1=3(an+1),
∴5+1=3(a1+1),解得a1=1.
∴数列{an+1}是等比数列,公比为3,首项为2.
∴an+1=2×3n-1,解得an=2×3n-1-1,
则S6=$\frac{2({3}^{6}-1)}{3-1}$-6=722.
故答案为:722.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
17.某社区对社区内50名70岁以上老人的身体健康状况和对平时锻炼身体的积极性进行了调查,统计数据如表所示:
(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是多少?抽到不积极锻炼身体且健康状况一般的老人的概率是多少?
(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表)
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| 积极锻炼身体 | 不积极锻炼身体 | 合计 | |
| 健康状况良好 | 18 | 7 | 25 |
| 健康状况一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表)
| P(k2>k) | 0.15 | 0.10 | 0.06 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
7.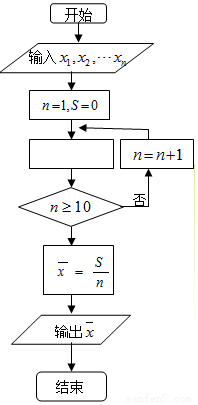 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )| A. | S=S+xn | B. | S=S+$\frac{{x}_{n}}{n}$ | C. | S=S+n | D. | S=S+$\frac{{x}_{n}}{10}$ |
14.某人的身份证号码是340304199803041290,随机掷一枚骰子,出现的点数是身份证上的数字的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
11.某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |