题目内容
若方程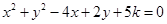 表示圆,则
表示圆,则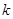 的取值范围是( )
的取值范围是( )
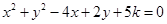 表示圆,则
表示圆,则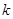 的取值范围是( )
的取值范围是( )A.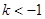 | B.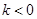 | C.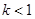 | D.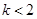 |
C
试题分析:根据圆的一般式方程x2+y2 +dx+ey+f=0( d2+e2-4f>0),列出不等式16+4-20k>0,求k的取值范围.解:关于x,y的方程
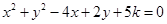 表示圆时,应有16+4-20k>0,解得 k<1,故答案为:C
表示圆时,应有16+4-20k>0,解得 k<1,故答案为:C点评:本题考查二元二次方程表示圆的条件,x2+y2 +dx+ey+f=0表示圆的充要条件是:d2+e2-4f>0

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
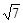 的圆的方程.
的圆的方程. 始终平分圆
始终平分圆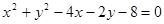 的周长,则
的周长,则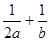 的最小值为
的最小值为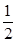



 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 为切点,
为切点, .若
.若 ,
, ,则
,则 的长为 .
的长为 . 
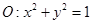 和点
和点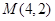 .
.
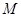 向⊙
向⊙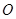 引切线
引切线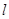 ,求直线
,求直线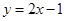 截得的弦长为4的⊙
截得的弦长为4的⊙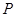 为(Ⅱ)中⊙
为(Ⅱ)中⊙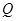 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点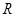 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由. 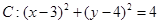 和直线
和直线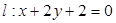 ,直线
,直线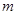 ,
,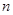 都经过圆C外定点A(1,0).
都经过圆C外定点A(1,0).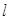 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,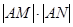 为定值.
为定值.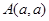 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数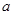 的取值范围为( )
的取值范围为( ) 或
或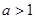
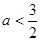
 或
或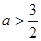
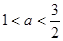
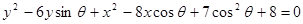 .
.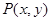 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求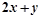 的取值范围.
的取值范围.