题目内容
已知⊙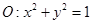 和点
和点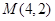 .
.

(Ⅰ)过点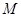 向⊙
向⊙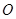 引切线
引切线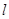 ,求直线
,求直线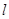 的方程;
的方程;
(Ⅱ)求以点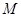 为圆心,且被直线
为圆心,且被直线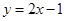 截得的弦长为4的⊙
截得的弦长为4的⊙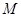 的方程;
的方程;
(Ⅲ)设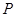 为(Ⅱ)中⊙
为(Ⅱ)中⊙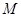 上任一点,过点
上任一点,过点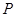 向⊙
向⊙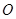 引切线,切点为
引切线,切点为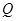 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点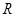 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
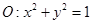 和点
和点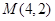 .
.
(Ⅰ)过点
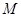 向⊙
向⊙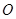 引切线
引切线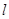 ,求直线
,求直线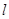 的方程;
的方程;(Ⅱ)求以点
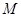 为圆心,且被直线
为圆心,且被直线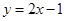 截得的弦长为4的⊙
截得的弦长为4的⊙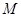 的方程;
的方程;(Ⅲ)设
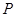 为(Ⅱ)中⊙
为(Ⅱ)中⊙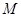 上任一点,过点
上任一点,过点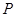 向⊙
向⊙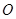 引切线,切点为
引切线,切点为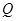 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点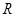 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由. (Ⅰ)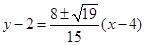 ;(Ⅱ)
;(Ⅱ)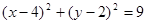
(Ⅲ)可以找到这样的定点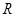 ,使得
,使得 为定值. 如点
为定值. 如点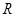 的坐标为
的坐标为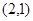 时,比值为
时,比值为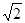 ;
;
点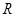 的坐标为
的坐标为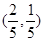 时,比值为
时,比值为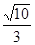
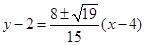 ;(Ⅱ)
;(Ⅱ)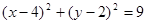
(Ⅲ)可以找到这样的定点
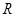 ,使得
,使得 为定值. 如点
为定值. 如点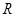 的坐标为
的坐标为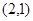 时,比值为
时,比值为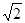 ;
;点
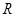 的坐标为
的坐标为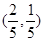 时,比值为
时,比值为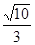
试题分析:(Ⅰ)设切线
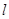 方程为
方程为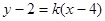 ,易得
,易得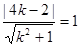 ,解得
,解得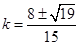 ……4分
……4分∴切线
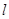 方程为
方程为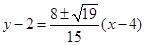
(Ⅱ)圆心到直线
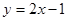 的距离为
的距离为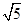 ,设圆的半径为
,设圆的半径为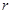 ,则
,则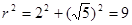 ,
,∴⊙
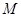 的方程为
的方程为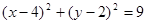
(Ⅲ)假设存在这样的点
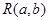 ,点
,点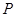 的坐标为
的坐标为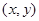 ,相应的定值为
,相应的定值为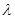 ,
,根据题意可得
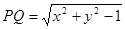 ,∴
,∴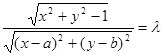 ,
,即
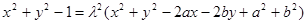 (*),
(*),又点
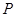 在圆上∴
在圆上∴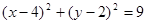 ,即
,即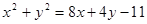 ,代入(*)式得:
,代入(*)式得: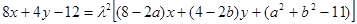
若系数对应相等,则等式恒成立,∴
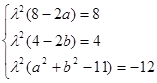 ,
,解得
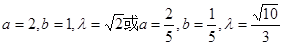
∴可以找到这样的定点
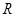 ,使得
,使得 为定值. 如点
为定值. 如点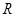 的坐标为
的坐标为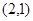 时,比值为
时,比值为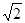 ;
;点
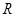 的坐标为
的坐标为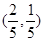 时,比值为
时,比值为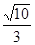
点评:中档题,涉及圆的题目,在近些年高考题中是屡有考查,求圆标准方程,研究直线与圆的位置关系。求圆的标准方程,主要考虑定义法、待定系数法。涉及直线于圆位置关系问题,往往应用韦达定理或充分利用“特征三角形”,通过半径、弦长一半、圆心到弦的距离,建立方程(组)。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
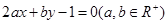 平分圆
平分圆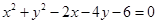 ,则
,则 的最小值是
的最小值是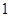
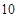
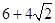
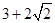
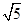
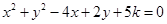 表示圆,则
表示圆,则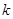 的取值范围是( )
的取值范围是( )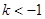
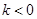
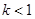
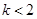
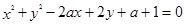 ,求圆心到直线
,求圆心到直线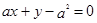 的距离的取值范围.
的距离的取值范围.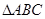 的外接圆的切线
的外接圆的切线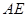 与
与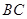 的延长线交于点
的延长线交于点 ,
,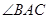 的平分线与
的平分线与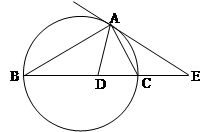
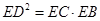
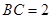 ,
, =1.求
=1.求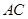 长.
长.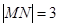 已知椭圆D:
已知椭圆D: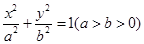 的焦距等于
的焦距等于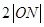 ,且过点
,且过点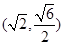

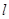 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.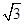 y-4=0相切,
y-4=0相切,