题目内容
11.把用数字0,1,2,3,4,5组成的没有重复数字的六位数,按照由小到大的顺序排列,设301245是该数列的第n项,则n的值为( )| A. | 239 | B. | 240 | C. | 241 | D. | 242 |
分析 由题意,首位是1,2没有重复数字的六位数,有${C}_{2}^{1}{A}_{5}^{5}$=240,301245是以3为首项,没有重复数字的六位数的最小数,即可得出结论.
解答 解:由题意,首位是1,2没有重复数字的六位数,
有${C}_{2}^{1}{A}_{5}^{5}$=240,301245是以3为首项,没有重复数字的六位数的最小数,
∴301245是该数列的第n项,n=241,
故选C.
点评 本题考查排列知识的运用,考查学生的计算能力,比较基础.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
17.已知函数f(x)是定义在R上的奇函数,且在区间[0,+∞)上单调递增,若$\frac{{|f(lnx)-f(ln\frac{1}{x})|}}{2}>f(1)$,则x的取值范围是( )
| A. | $(-∞\;,\;\;\frac{1}{e})$ | B. | (e,+∞) | C. | $(\frac{1}{e}\;,\;\;e)$ | D. | $(0\;,\;\;\frac{1}{e})$∪(e,+∞) |
6.设函数f(x)=|sin(x+$\frac{π}{3}$)|(x∈R),则f(x)( )
| A. | 在区间[$\frac{2π}{3}$,$\frac{7π}{6}$]上是增函数 | B. | 在区间[-π,-$\frac{π}{2}$]上是减函数 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{4}$]上是增函数 | D. | 在区间[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数 |
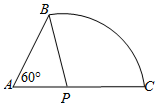 某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P,半径为PB的一段圆弧BC构成,其中∠BAC=60°.
某柱体实心铜制零件的截面边长是长度为55毫米线段AB和88毫米的线段AC以及圆心为P,半径为PB的一段圆弧BC构成,其中∠BAC=60°. 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O 的直径AB=2,C是弧$\widehat{AB}$的中点,D为AC的中点.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O 的直径AB=2,C是弧$\widehat{AB}$的中点,D为AC的中点.