题目内容
若双曲线 与直线y=
与直线y= x无交点,则离心率e的取值范围( )
x无交点,则离心率e的取值范围( )A.(1,2)
B.(1,2]
C.(1,
 )
)D.(1,
 ]
]
【答案】分析:根据题意,双曲线位于一、三象限的渐近线的斜率小于或等于 ,满足
,满足 ≤
≤ ,由此结合双曲线基本量的平方关系和离心率的公式,化简整理即可得到该双曲线的离心率e的取值范围.
,由此结合双曲线基本量的平方关系和离心率的公式,化简整理即可得到该双曲线的离心率e的取值范围.
解答:解:∵双曲线 与直线y=
与直线y= x无交点,
x无交点,
∴双曲线的渐近线方程y= x,满足
x,满足 ≤
≤
得b≤ a,两边平方得b2≤3a2,即c2-a2≤3a2,
a,两边平方得b2≤3a2,即c2-a2≤3a2,
∴c2≤4a2,得 ≤4即e2≤4,
≤4即e2≤4,
∵双曲线的离心率e为大于1的正数
∴1<e≤2,
故选B
点评:本题给出双曲线与直线y= x无交点,求双曲线离心率e的取值范围,考查了双曲线的标准方程和简单几何性质等知识,属于基础题.
x无交点,求双曲线离心率e的取值范围,考查了双曲线的标准方程和简单几何性质等知识,属于基础题.
 ,满足
,满足 ≤
≤ ,由此结合双曲线基本量的平方关系和离心率的公式,化简整理即可得到该双曲线的离心率e的取值范围.
,由此结合双曲线基本量的平方关系和离心率的公式,化简整理即可得到该双曲线的离心率e的取值范围.解答:解:∵双曲线
 与直线y=
与直线y= x无交点,
x无交点,∴双曲线的渐近线方程y=
 x,满足
x,满足 ≤
≤
得b≤
 a,两边平方得b2≤3a2,即c2-a2≤3a2,
a,两边平方得b2≤3a2,即c2-a2≤3a2,∴c2≤4a2,得
 ≤4即e2≤4,
≤4即e2≤4,∵双曲线的离心率e为大于1的正数
∴1<e≤2,
故选B
点评:本题给出双曲线与直线y=
 x无交点,求双曲线离心率e的取值范围,考查了双曲线的标准方程和简单几何性质等知识,属于基础题.
x无交点,求双曲线离心率e的取值范围,考查了双曲线的标准方程和简单几何性质等知识,属于基础题. 
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
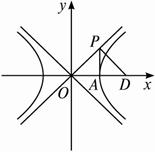
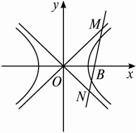
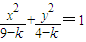 .
.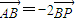 ?若存在,求出k的值;若不存在,说明理由;
?若存在,求出k的值;若不存在,说明理由;