题目内容
已知二次曲线Ck的方程:| x2 |
| 9-k |
| y2 |
| 4-k |
(1)分别求出方程表示椭圆和双曲线的条件;
(2)对于点P(-1,0),是否存在曲线Ck交直线y=x+1于A、B两点,使得
| AB |
| BP |
(3)已知Ck与直线y=x+1有公共点,求其中实轴最长的双曲线方程.
分析:(1)当且仅当
时,方程表示椭圆;当且仅当(9-k)(4-k)<0,方程表示双曲线.
(2)联立
,得:(13-2k)x2+2(9-k)x+(9-k)(k-3)=0有两个实根,△=4(9-k)•2(k-4)(k-6)>0⇒k<4或6<k<9.由此能够导出k不存在.
(3)因为ck为双曲线,所以4<k<9,由△≥0,可得6≤k<9.由此能求出实轴最长的双曲线方程.
|
(2)联立
|
(3)因为ck为双曲线,所以4<k<9,由△≥0,可得6≤k<9.由此能求出实轴最长的双曲线方程.
解答:解:(1)当且仅当
即 k<4时,方程表示椭圆;--------------------------(2分)
当且仅当(9-k)(4-k)<0,即4<k<9时,方程表示双曲线.---------------------(4分)
(2)联立
得:(13-2k)x2+2(9-k)x+(9-k)(k-3)=0有两个实根-----------------------------(6分)
△=4(9-k)•2(k-4)(k-6)>0⇒k<4或6<k<9----------------(8分)
设:A(x1,y1),B(x2,y2),由
=-2
,
得到
----------------(10分)
⇒
=-2,
得到 k=4,所以k不存在-----------------------------------(12分)
(3)因为ck为双曲线,所以4<k<9由△≥0,可得6≤k<9--------------------------(15分)
双曲线实轴2a=9-k≤3,所以最长时k=6,此时双曲线方程为
-
=1---(18分)
|
当且仅当(9-k)(4-k)<0,即4<k<9时,方程表示双曲线.---------------------(4分)
(2)联立
|
得:(13-2k)x2+2(9-k)x+(9-k)(k-3)=0有两个实根-----------------------------(6分)
△=4(9-k)•2(k-4)(k-6)>0⇒k<4或6<k<9----------------(8分)
设:A(x1,y1),B(x2,y2),由
| AB |
| BP |
得到
|
⇒
| -2(9-k) |
| 13-2k |
得到 k=4,所以k不存在-----------------------------------(12分)
(3)因为ck为双曲线,所以4<k<9由△≥0,可得6≤k<9--------------------------(15分)
双曲线实轴2a=9-k≤3,所以最长时k=6,此时双曲线方程为
| x2 |
| 3 |
| y2 |
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
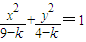 .
.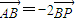 ?若存在,求出k的值;若不存在,说明理由;
?若存在,求出k的值;若不存在,说明理由;