题目内容
已知函数 .当
.当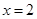 时,函数
时,函数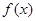 取得极值
取得极值 .
.
(1)求函数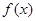 的解析式;
的解析式;
(2)若方程 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围.
 .当
.当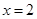 时,函数
时,函数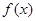 取得极值
取得极值 .
.(1)求函数
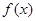 的解析式;
的解析式;(2)若方程
 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)先求出函数
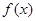 的导数
的导数 ,进而根据当
,进而根据当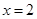 时,函数
时,函数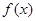 取得极值
取得极值 ,得到
,得到 即
即 ,求解方程组即可得到
,求解方程组即可得到 的值,从而可写出函数
的值,从而可写出函数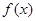 的解析式;(2)先根据(1)确定的函数
的解析式;(2)先根据(1)确定的函数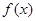 的解析式求出导函数,然后确定函数的极大值及极小值,依题意要使方程
的解析式求出导函数,然后确定函数的极大值及极小值,依题意要使方程 有3个解,只须
有3个解,只须 在两个极值之间即可.
在两个极值之间即可.试题解析:(1)因为
 ,而当
,而当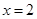 时,函数
时,函数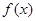 取得极值
取得极值
所以
 ,
, 即
即 ,由此可解得
,由此可解得 ,
,
所以函数的解析式为

(2)因为
 ,
,
由
 或
或
所以
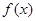 在
在 处取得极大值
处取得极大值 ,在
,在 处取得极小值
处取得极小值 ----12分
----12分要满足函数
 有3个解,须有
有3个解,须有 .
.
练习册系列答案
相关题目
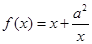 ,
, ,其中
,其中 .
.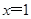 是函数
是函数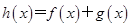 的极值点,求实数
的极值点,求实数 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数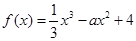 ,且
,且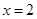 是函数
是函数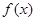 的一个极小值点.
的一个极小值点.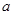 的值;
的值;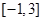 上的最大值和最小值.
上的最大值和最小值.
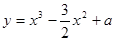 在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________
在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是__________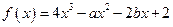 处有极值,则ab的最大值等于( ).
处有极值,则ab的最大值等于( ). 已知
已知 时取得极值,则
时取得极值,则 的值等于( )
的值等于( )