题目内容
三角形ABC,顶点A(1,0),B(2,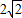 ),C(3,0),该三角形的内切圆方程为( )
),C(3,0),该三角形的内切圆方程为( )A.
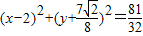
B.
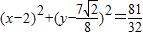
C.
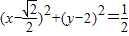
D.
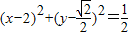
【答案】分析:根据A、B、C的坐标算出三角形的面积S=2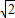 、周长为8,由此算出内切圆半径r=
、周长为8,由此算出内切圆半径r=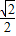 .再求出∠BAC平分线与∠BCA平分线的交点坐标(2,
.再求出∠BAC平分线与∠BCA平分线的交点坐标(2,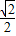 ),利用圆的标准方程列式,即可得到该三角形的内切圆方程.
),利用圆的标准方程列式,即可得到该三角形的内切圆方程.
解答:解:∵A(1,0),B(2,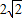 ),C(3,0),
),C(3,0),
∴可得|AB|=3,|AC|=2,|BC|=3
三角形的面积S= |AC|•yB=2
|AC|•yB=2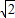 ,周长为3+2+3=8
,周长为3+2+3=8
因此,三角形的内切圆半径r=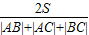 =
=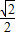
又∵圆心为∠BAC平分线与∠BCA平分线的交点
∴算出圆心坐标为(2,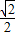 ),
),
可得该三角形的内切圆方程为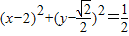
故选:D
点评:本题给出三角形的三个顶点A、B、C的坐标,求它的内切圆方程.着重考查了直线的方程、三角形内切圆的性质、圆的标准方程等知识,属于中档题.
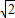 、周长为8,由此算出内切圆半径r=
、周长为8,由此算出内切圆半径r=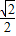 .再求出∠BAC平分线与∠BCA平分线的交点坐标(2,
.再求出∠BAC平分线与∠BCA平分线的交点坐标(2,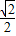 ),利用圆的标准方程列式,即可得到该三角形的内切圆方程.
),利用圆的标准方程列式,即可得到该三角形的内切圆方程.解答:解:∵A(1,0),B(2,
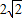 ),C(3,0),
),C(3,0),∴可得|AB|=3,|AC|=2,|BC|=3
三角形的面积S=
 |AC|•yB=2
|AC|•yB=2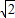 ,周长为3+2+3=8
,周长为3+2+3=8因此,三角形的内切圆半径r=
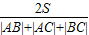 =
=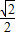
又∵圆心为∠BAC平分线与∠BCA平分线的交点
∴算出圆心坐标为(2,
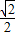 ),
),可得该三角形的内切圆方程为
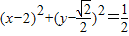
故选:D
点评:本题给出三角形的三个顶点A、B、C的坐标,求它的内切圆方程.着重考查了直线的方程、三角形内切圆的性质、圆的标准方程等知识,属于中档题.

练习册系列答案
相关题目
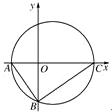 如图,直角三角形ABC的顶点A的坐标为(-2,0),直角顶点B的坐标为(0,-2
如图,直角三角形ABC的顶点A的坐标为(-2,0),直角顶点B的坐标为(0,-2 椭圆
椭圆