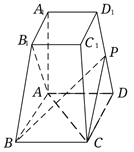
题目内容
【题目】关于异面直线![]() ,有下列四个命题:
,有下列四个命题:
(1)过直线![]() 有且仅有一个平面
有且仅有一个平面![]() ,使
,使![]() //
//![]() ;
;
(2)过直线![]() 有且仅有一个平面
有且仅有一个平面![]() ,使
,使![]()
![]()
![]() ;
;
(3)在空间中存在平面![]() ,使
,使![]() //
//![]() ,
,![]() //
//![]() ;
;
(4)在空间中不存在平面![]() ,使
,使![]()
![]()
![]() ,
,![]()
![]()
![]() ;
;
其中正确命题的序号是____________.
【答案】(1)(3)(4)
【解析】
利用线面平行的性质可证(1)成立,用反证法可得(2)错误,(4)正确,利用线面平行的判定定理可得(3)正确.
在直线![]() 选一点
选一点![]() ,过
,过![]() 作直线
作直线![]() ,由公理3的推论可知存在平面
,由公理3的推论可知存在平面![]() ,使得
,使得![]() ,因
,因![]() 异面,故
异面,故![]() ,所以
,所以![]() ,若存在不同的平面
,若存在不同的平面![]() ,使得
,使得![]() ,则
,则![]() ,故
,故![]() ,与
,与![]() 异面矛盾,故(1)正确.
异面矛盾,故(1)正确.
对于(2),若存在平面![]() ,使得
,使得![]() ,因
,因![]() ,故
,故![]() ,所以当
,所以当![]() 不垂直时,(2)就不成立,故(2)错.
不垂直时,(2)就不成立,故(2)错.
对于(4),如存在平面![]() ,使得
,使得![]() ,则
,则![]() ,与
,与![]() 异面矛盾,故(4)正确.
异面矛盾,故(4)正确.
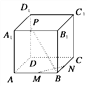
对于(3),在空间中取![]() ,过
,过![]() 分别作
分别作![]() 的平行线
的平行线![]() ,设相交直线
,设相交直线![]() 确定的平面为
确定的平面为![]() (如果
(如果![]() 中有一条直线在该平面中,可平移该平面使得
中有一条直线在该平面中,可平移该平面使得![]() 均在平面外),则
均在平面外),则![]() ,故(3)正确.
,故(3)正确.
综上,填(1)(3)(4).

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目