题目内容
14.已知$\overrightarrow{a}$=(2,-3,1),$\overline{b}$=(2,0,3),$\overrightarrow{c}$=(0,1,-2),则$\overrightarrow{a}$+4$\overrightarrow{b}$-3$\overrightarrow{c}$等于( )| A. | (4,-4,6) | B. | (-6,-6,-5) | C. | (10,0,7) | D. | (10,-6,19) |
分析 使用向量的坐标运算计算.
解答 解:$\overrightarrow{a}$+4$\overrightarrow{b}$-3$\overrightarrow{c}$=(2,-3,1)+(8,0,12)-(0,3,-6)=(10,-6,19).
故选:D.
点评 本题考查了空间向量的坐标运算,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
2.若不等式ax2+5x-2>0的解集是{x|$\frac{1}{2}$<x<2},则a的值为( )
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
19.抛物线y=-$\frac{1}{2}$x2的焦点坐标为( )
| A. | (-$\frac{1}{2}$,0) | B. | (0,-$\frac{1}{4}$) | C. | (0,-$\frac{1}{2}$) | D. | (0,-1) |
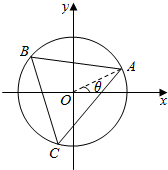 如图,正三角形ABC内接于单位圆O,设∠AOx=θ,A(xA,yA),B(xB,yB),C(xC.yC).
如图,正三角形ABC内接于单位圆O,设∠AOx=θ,A(xA,yA),B(xB,yB),C(xC.yC).