题目内容
数列1×4,2×5,3×6,…,n×(n+3),…则它的前n项和Sn=________.

分析:由题设条件知:an=n×(n+3)=n2+3n,Sn=(1+3×1)+(4+3×2)+(9+3×3)+…+(n2+3n)=(12+22+32+…+n2)+3(1+2+3+…+n)=
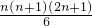 +
+ ;化简可得答案.
;化简可得答案.解答:∵an=n×(n+3)=n2+3n,
∴Sn=a1+a2+a3+…+an
=(1+3×1)+(4+3×2)+(9+3×3)+…+(n2+3n)
=(12+22+32+…+n2)+3(1+2+3+…+n)
=
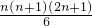 +
+
=
 .
.答案:
 .
.点评:本题考查数列的性质和应用,解题时要认真审题,仔细求解.

练习册系列答案
相关题目
下列说法正确的是( )
| A、数列1,3,5,7可表示为{1,3,5,7} | ||||
| B、数列1,0,-1,-2与数列-2,-1,0,1是相同的数列 | ||||
C、数列{
| ||||
| D、数列0,2,4,6,…可记为{2n} |