题目内容
数列{an}中a1=2, ,{bn}中
,{bn}中 .
.
(1)求证:数列{bn}为等比数列,并求出其通项公式;
(2)当n≥3(n∈N*)时,证明: .
.
证明:(1)由
 又
又
∴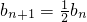
又n=1时,
∴{bn}为等比数列,b1=2, ,∴
,∴
(2)∵
∴
先证:
当n为偶数时,显然成立;
当n为奇数时,即证
而当n≥3时,2n>n+1也成立,故
∴
令 ①
① ②
②
①-②:
 =
=
∴
分析:(1)根据{bn}中 ,
, ,可得
,可得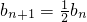 ,从而可证数列{bn}为等比数列,并求出其通项公式;
,从而可证数列{bn}为等比数列,并求出其通项公式;
(2)先将通项化简可得 ,从而有
,从而有 ,先证:
,先证:
,从而有
令 ①
① ②,利用错位相减法即可求解.
②,利用错位相减法即可求解.
点评:本题以数列为载体,考查等比数列,考查数列与不等式,考查错位相减法,综合性强,难度大.

 又
又
∴
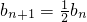
又n=1时,

∴{bn}为等比数列,b1=2,
 ,∴
,∴
(2)∵

∴

先证:

当n为偶数时,显然成立;
当n为奇数时,即证

而当n≥3时,2n>n+1也成立,故

∴

令
 ①
① ②
②①-②:

 =
=
∴

分析:(1)根据{bn}中
 ,
, ,可得
,可得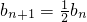 ,从而可证数列{bn}为等比数列,并求出其通项公式;
,从而可证数列{bn}为等比数列,并求出其通项公式;(2)先将通项化简可得
 ,从而有
,从而有 ,先证:
,先证:
,从而有

令
 ①
① ②,利用错位相减法即可求解.
②,利用错位相减法即可求解.点评:本题以数列为载体,考查等比数列,考查数列与不等式,考查错位相减法,综合性强,难度大.

练习册系列答案
相关题目