题目内容
17.有10本不同的书紧贴着依次立放在书架上,摆成上层3本下层7本,现要从下层7本中任取2本再随机分别调整到上层,若其他书本的相对顺序不变,则上层新增的2本书不相邻的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
分析 分两种情况:一是抽出来的2本书连在一起插入上层3本书的四个空档中,共有${A}_{2}^{2}{A}_{4}^{1}$=8种,二是抽出来的2本书分开插入上层3本书的四个空档中,共有${A}_{4}^{2}$种,由此能求出上层新增的2本书不相邻的概率.
解答 解:分两种情况:
一是抽出来的2本书连在一起插入上层3本书的四个空档中,共有${A}_{2}^{2}{A}_{4}^{1}$=8种,
二是抽出来的2本书分开插入上层3本书的四个空档中,共有${A}_{4}^{2}$种,
上层新增的2本书不相邻的概率为:
p=$\frac{{A}_{4}^{2}}{{A}_{4}^{2}+{A}_{2}^{2}{A}_{4}^{1}}$=$\frac{3}{5}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
8.在△ABC中,若sinA:sinB:sinC=2:3:4,则最大角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
5.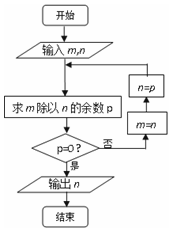 执行右面的程序框图,如果输入m=72,n=30,则输出的n是( )
执行右面的程序框图,如果输入m=72,n=30,则输出的n是( )
 执行右面的程序框图,如果输入m=72,n=30,则输出的n是( )
执行右面的程序框图,如果输入m=72,n=30,则输出的n是( )| A. | 12 | B. | 6 | C. | 3 | D. | 0 |
7.对函数f(x),如果存在x0≠0使得f(x0)=-f(-x0),则称(x0,f(x0))与(-x0,f(-x0))为函数图象的一组奇对称点.若f(x)=ex-a(e为自然数的底数)存在奇对称点,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (e,+∞) | D. | [1,+∞) |
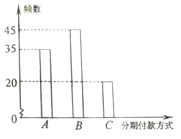 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.