题目内容
已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() (
(![]() 为常数)。
为常数)。
(1) 求函数![]() 的解析式;
的解析式;
(2) 当![]() 时,求
时,求![]() 在
在![]() 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的![]() ,并猜想
,并猜想![]() 在
在![]() 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3) 当![]() 时,证明:函数
时,证明:函数![]() 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线![]() 上。
上。
解:(1) ![]() 时,
时,![]() , 则
, 则 ![]()
∵函数![]() 是定义在
是定义在![]() 上的奇函数,即
上的奇函数,即![]()
∴![]() ,即
,即 ![]() , 3分
, 3分
又可知 ![]() 。 4分
。 4分
∴函数![]() 的解析式为
的解析式为 ![]() ; 6分
; 6分
(2) ![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]()
![]()
![]() 。
。
∵  9分
9分
∴![]() ,即
,即 ![]()
![]() ,
,
![]()
![]()
![]() 。 11分
。 11分
∴猜想![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为![]() 。 12分
。 12分
(3) ![]() 时,任取
时,任取![]() ,
,
∵![]()
∴![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ,即
,即![]() 14分
14分
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() , 16分
, 16分
且函数![]() 的图像是连续的曲线,
的图像是连续的曲线,
∴当![]() 时,函数
时,函数![]() 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线![]() 上。 18分
上。 18分

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若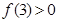 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;