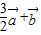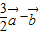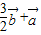题目内容
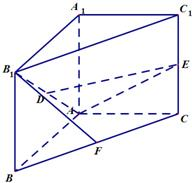 如图:△ABC为等腰直角三角形,∠BAC=90°,将△ABC沿它的垂直方向平移至△A1B1C1,且AB=AA1=4,D、E、F分别为B1A、C1C、BC的中点.
如图:△ABC为等腰直角三角形,∠BAC=90°,将△ABC沿它的垂直方向平移至△A1B1C1,且AB=AA1=4,D、E、F分别为B1A、C1C、BC的中点.(1)求证:DE∥平面ABC;
(2)求直线AF与平面AB1E所成角的大小.
分析:(1)取AB的中点M,连接MD,CD,由MD是△ABB1的中位线,知MD∥BB1,MD=
BB1,由EC∥BB1,EC=
BB1,知四边形CEDM是平行四边形,由此能证明DE∥平面ABC.
(2)建立空间直角坐标系A-xyz,可求得平面AEB1的一法向量
为(2,1,-2),又
=(2,2,0)由此能求出直线AF与平面AEB1所成角.
| 1 |
| 2 |
| 1 |
| 2 |
(2)建立空间直角坐标系A-xyz,可求得平面AEB1的一法向量
| n |
| AF |
解答:(1)证明:取AB的中点M,连接MD,CD,
∵MD是△ABB1的中位线,
∴MD∥BB1,MD=
BB1,
又∵EC∥BB1,EC=
BB1,
∴MD∥ED,MD=ED,
∴四边形CEDM是平行四边形,
∴DE∥CMDE?平面ABCCM?平面ABC,
∴DE∥平面ABC.…(5分)
(2)解:建立如图所示的空间直角坐标系A-xyz,
∵AB=AA1=4,D、E、F分别为B1A、C1C、BC的中点.
∴A(0,0,0),E(0,4,2),B1(4,0,4),
∴
=(0,4,2),
=(4,0,4),
设面AEB1的一法向量
=(x,y,z),
∵
•
=0,
•
=0,
∴
,
∴
=(2,1,-2)
又
=(2,2,0),
∴sinθ=
=
=
,
所以直线AF与平面AEB1所成角为
.…(10分)
∵MD是△ABB1的中位线,
∴MD∥BB1,MD=
| 1 |
| 2 |
又∵EC∥BB1,EC=
| 1 |
| 2 |
∴MD∥ED,MD=ED,
∴四边形CEDM是平行四边形,
∴DE∥CMDE?平面ABCCM?平面ABC,
∴DE∥平面ABC.…(5分)
(2)解:建立如图所示的空间直角坐标系A-xyz,
∵AB=AA1=4,D、E、F分别为B1A、C1C、BC的中点.
∴A(0,0,0),E(0,4,2),B1(4,0,4),

∴
| AE |
| AB1 |
设面AEB1的一法向量
| n |
∵
| n |
| AE |
| n |
| AB1 |
∴
|
∴
| n |
又
| AF |
∴sinθ=
|
| ||||
|
|
| 6 | ||
2
|
| ||
| 2 |
所以直线AF与平面AEB1所成角为
| π |
| 4 |
点评:本题考查直线和平面平行的证明和直线与平面所成角的求法.解题时要认真审题,注意合理地把立体问题转化为平面问题,注意向量法的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
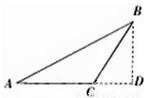
如图,△ABC为等腰三角形,∠A=∠B=30°,设
=
,
=
,AC边上的高为BD.若用
,
表示
,则表达式为( )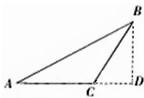
| AB |
| a |
| AC |
| b |
| a |
| b |
| BD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
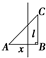 如图,△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,直线l截这个三角形所得的位于直线在右方的图形面积为y,点A到直线l的距离为x,则y=f(x)的图象大致为四个选项中的( )
如图,△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,直线l截这个三角形所得的位于直线在右方的图形面积为y,点A到直线l的距离为x,则y=f(x)的图象大致为四个选项中的( )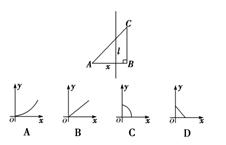
 ,
, ,AC边上的高为BD.若用
,AC边上的高为BD.若用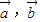 表示
表示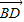 ,则表达式为( )
,则表达式为( )