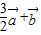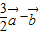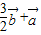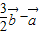题目内容
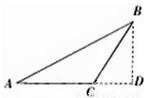
如图，△ABC为等腰三角形，∠A=∠B=30°，设
=
，
=
，AC边上的高为BD．若用
，
表示
，则表达式为（ ）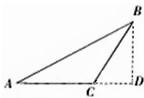
| AB |
| a |
| AC |
| b |
| a |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析：根据所给的三角形是等腰三角形和角的度数，得到三角形BCD是一个含有30°角的三角形，有边之间的关系，把要求的向量从起点出发，绕着三角形的边到终点，根据三角形边之间的关系得到结果．
解答：解：∵在三角形BCD中由∠A=∠ABC=30°
∴CD=
BC，
∵
=
+
，
∴
=
+
+
=-
+
+
=-
+
，
故选D．
∴CD=
| 1 |
| 2 |
∵
| BD |
| BA |
| AD |
∴
| BD |
| BA |
| AC |
| CD |
| a |
| b |
| 1 |
| 2 |
| b |
=-
| a |
| 3 |
| 2 |
| b |
故选D．
点评：用一组向量来表示一个向量，是以后解题过程中常见到的，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题．
练习册系列答案
相关题目
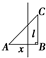如图，△ABC为等腰直角三角形，直线l与AB相交且l⊥AB，直线l截这个三角形所得的位于直线在右方的图形面积为y，点A到直线l的距离为x，则y=f（x）的图象大致为四个选项中的（ ）
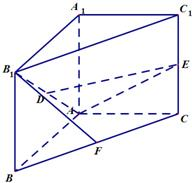如图：△ABC为等腰直角三角形，∠BAC=90°，将△ABC沿它的垂直方向平移至△A1B1C1，且AB=AA1=4，D、E、F分别为B1A、C1C、BC的中点．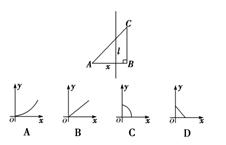
，
，AC边上的高为BD．若用
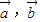表示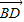
，则表达式为（ ）
