题目内容
(3分)(2011•重庆)已知 ,则a=( )
,则a=( )
| A.1 | B.2 | C.3 | D.6 |
D
解析试题分析:先将极限式通分化简,得到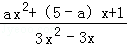 ,分子分母同时除以x2,再取极限即可.
,分子分母同时除以x2,再取极限即可.
解:原式=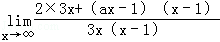
=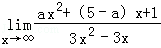 (分子分母同时除以x2)
(分子分母同时除以x2)
=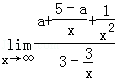
=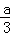 =2
=2
∴a=6
故答案选D.
点评:关于高中极限式的运算,一般要先化简再代值取极限,本题中运用到的分子分母同时除以某个数或某个式子,是极限运算中常用的计算技巧.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
(5分)(2011•湖北)若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=ex,则g(x)=( )
| A.ex﹣e﹣x | B. (ex+e﹣x) (ex+e﹣x) | C. (e﹣x﹣ex) (e﹣x﹣ex) | D. (ex﹣e﹣x) (ex﹣e﹣x) |
对任意实数 ,
,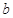 定义运算“⊙”:
定义运算“⊙”: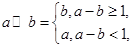 设
设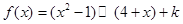 ,若函数
,若函数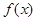 的图象与
的图象与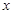 轴恰有三个交点,则
轴恰有三个交点,则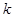 的取值范围是( )
的取值范围是( )
A.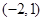 | B.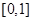 |
C.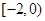 | D.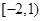 |
函数 的定义域为
的定义域为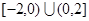 ,其图像上任一点
,其图像上任一点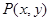 都位于椭圆
都位于椭圆 :
: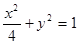 上,下列判断①函数
上,下列判断①函数 一定是偶函数;②函数
一定是偶函数;②函数 可能既不是偶函数,也不是奇函数;③函数
可能既不是偶函数,也不是奇函数;③函数 可能是奇函数;④函数
可能是奇函数;④函数 如果是偶函数,则值域是
如果是偶函数,则值域是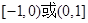 ;⑤函数
;⑤函数 值域是
值域是 ,则一定是奇函数.其中正确的命题个数有( )个
,则一定是奇函数.其中正确的命题个数有( )个
| A.1 | B.2 | C.3 | D.4 |
[2013·湖北荆门期末]函数f(x)=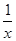 ln(
ln(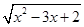 +
+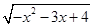 )的定义域为( )
)的定义域为( )
| A.(-∞,-4]∪(2,+∞) |
| B.(-4,0)∪(0,1) |
| C.[-4,0)∪(0,1] |
| D.[-4,0)∪(0,1) |
已知函数f(x)= 是(-∞,+∞)上的减函数,则a的取值范围是
是(-∞,+∞)上的减函数,则a的取值范围是
( )
| A.(0,3) | B.(0,3] | C.(0,2) | D.(0,2] |
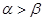 ,则下列结论正确的是( )
,则下列结论正确的是( )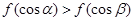
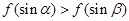
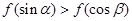

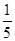 ,则f(log220)的值为( )
,则f(log220)的值为( )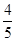
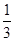 )的x的取值范围是( )
)的x的取值范围是( )