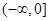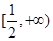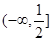题目内容
已知奇函数f(x)在[-1,0]上为单调递减函数,又α、β为锐角三角形两内角且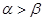 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.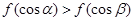 | B.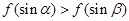 |
C.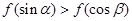 | D. |
B
解析试题分析:∵奇函数 在[-1,0]上是减函数,∴
在[-1,0]上是减函数,∴ 在[0,1]上是增函数,又∵
在[0,1]上是增函数,又∵ 是锐角三角形两内角,∴
是锐角三角形两内角,∴ ,又∵
,又∵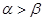 ,∴
,∴ ,
,
∴ ,B正确,A错误;.对于C,D:∵
,B正确,A错误;.对于C,D:∵ 为锐角三角形两内角,∴
为锐角三角形两内角,∴ ,∴
,∴ ,即
,即 ,∴
,∴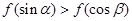 ,
,
∴C正确,D错误.
考点:1、奇函数单调性的判断;2、三角函数值的大小比较.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知函数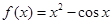 ,则
,则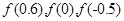 的大小关系是( )
的大小关系是( )
A.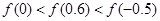 |
B.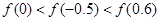 |
C.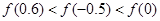 |
D.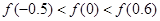 |
定义在R上的函数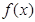 和
和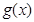 的导函数分别为
的导函数分别为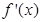 ,
,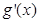 ,则下面结论正确的是( )
,则下面结论正确的是( )
①若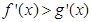 ,则函数
,则函数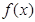 的图象在函数
的图象在函数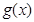 的图象上方;
的图象上方;
②若函数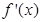 与
与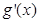 的图象关于直线
的图象关于直线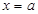 对称,则函数
对称,则函数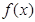 与
与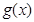 的图象关于点(
的图象关于点(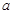 ,0)对称;
,0)对称;
③函数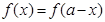 ,则
,则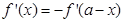 ;
;
④若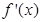 是增函数,则
是增函数,则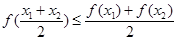 .
.
| A.①② | B.①②③ | C.③④ | D.②③④ |
设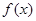 为定义域在R上的偶函数,且
为定义域在R上的偶函数,且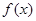 在
在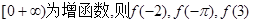 的大小顺序为( )
的大小顺序为( )
A.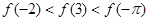 | B.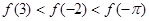 |
C. | D.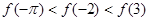 |
(3分)(2011•重庆)已知 ,则a=( )
,则a=( )
| A.1 | B.2 | C.3 | D.6 |
若函数f(x)、g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
若f(x)对于任意实数x恒有2f(x)-f(-x)=3x+1,则f(x)=( )
| A.x-1 | B.x+1 | C.2x+1 | D.3x+3 |
[2014·湖南六校联考]设x1,x2是方程ln|x-2|=m(m为实数)的两根,则x1+x2的值为( )
| A.4 | B.2 | C.-4 | D.与m有关 |
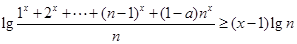 对任意不大于1的实数x和大于1的正整数n都成立,则实数a的取值范围是( )
对任意不大于1的实数x和大于1的正整数n都成立,则实数a的取值范围是( )