题目内容
(本小题满分12分)已知函数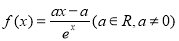 .
.
(1)当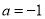 时,求函数
时,求函数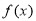 的极值;
的极值;
(2)若函数 没有零点,求实数
没有零点,求实数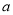 的取值范围.
的取值范围.
(1)极小值 ,无极大值;(2)
,无极大值;(2) .
.
【解析】
试题分析:(1)当 时,
时, ,通过求导判断
,通过求导判断 的单调性即可求得
的单调性即可求得 的极值;(2)通过求导判断
的极值;(2)通过求导判断 的单调性与极值,从而确定
的单调性与极值,从而确定 没有零点时
没有零点时 的取值范围.
的取值范围.
试题解析:(1)当 时,
时, ,
, ,
,
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
∴ 的极小值为
的极小值为 ,无极大值; (2)当
,无极大值; (2)当 时,
时, ,
, 的情况如下表:
的情况如下表:
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
若使 没有零点,当且仅当
没有零点,当且仅当 ,解得
,解得 ,∴此时
,∴此时 ,当
,当 时,
时, ,
, 的情况如下表:
的情况如下表:
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 |
∵ ,且
,且 ,此时
,此时 总存在零点,
总存在零点,
综上所述,实数 的取值范围是
的取值范围是 .
.
考点:1.利用导数求函数的极值;2.分类讨论的数学思想.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目













 ,
, ,则
,则 .
.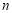 个正数
个正数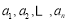 满足
满足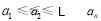 (
(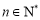 且
且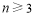 ).
).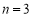 时,证明:
时,证明: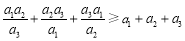 ;
;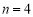 时,不等式
时,不等式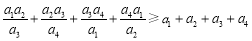 也成立,请你将其推广到
也成立,请你将其推广到 在点
在点 处的切线方程为 .
处的切线方程为 . (
( ,i为虚数单位),若
,i为虚数单位),若 ,则
,则 的值为 .
的值为 . 在
在 上有最大值
上有最大值 ;
; 在
在 上是减函数;
上是减函数; ,使函数
,使函数 为奇函数;
为奇函数; ,
, ,满足
,满足 ”
” ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 满足
满足 ,
, ,则该数列的前
,则该数列的前 项的乘积
项的乘积 _________.
_________.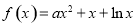 (
(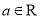 ).
).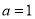 时,求函数
时,求函数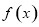 的图象在点
的图象在点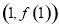 处的切线方程;
处的切线方程;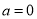 ,求证:当
,求证:当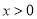 时,
时,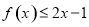 ;
; 恰有两个零点
恰有两个零点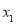 ,
,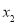 (
(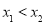 ),求实数
),求实数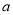 的取值范围.
的取值范围.