题目内容
(本小题满分14分)已知函数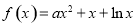 (
(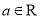 ).
).
(1)当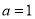 时,求函数
时,求函数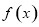 的图象在点
的图象在点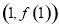 处的切线方程;
处的切线方程;
(2)设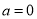 ,求证:当
,求证:当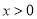 时,
时,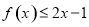 ;
;
(3)若函数 恰有两个零点
恰有两个零点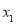 ,
,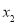 (
(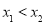 ),求实数
),求实数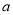 的取值范围.
的取值范围.
(1)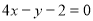 ;(2)见解析;(3)实数
;(2)见解析;(3)实数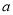 的取值范围是
的取值范围是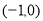 .
.
【解析】
试题分析:(1)当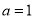 时,
时,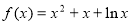 ,
, 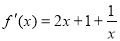 ,进一步求函数在切点处的导数,即切线的斜率,得到切线方程.
,进一步求函数在切点处的导数,即切线的斜率,得到切线方程.
(2)当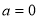 时,设
时,设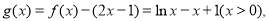
应用导数研究函数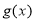 的单调性得:函数
的单调性得:函数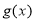 在
在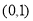 上单调递增,在
上单调递增,在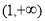 上是单调递减
上是单调递减
根据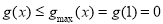 ,即得证.
,即得证.
(3)由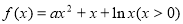 得
得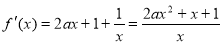 .
.
讨论当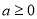 时,当
时,当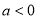 时,
时,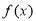 在
在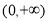 的单调性,确定
的单调性,确定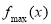 .
.
通过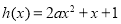 ,由
,由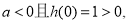 得
得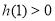 解得
解得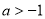 ,得到实数
,得到实数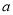 的取值范围.
的取值范围.
试题解析:(1)当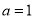 时,
时,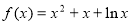 ,
, 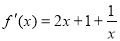
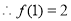 ,
,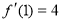
函数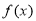 的图象在点
的图象在点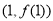 处的切线方程为
处的切线方程为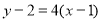
即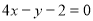 4分
4分
(2)当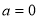 时,设
时,设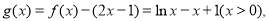
则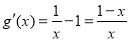 ,
,
当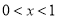 时,
时,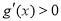 ;当
;当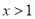 时,
时,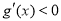 .
.
因此,函数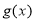 在
在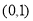 上单调递增,在
上单调递增,在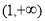 上是单调递减
上是单调递减
得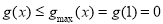 ,即
,即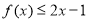 . 9分
. 9分
(3)由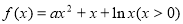 得
得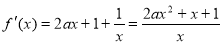 .
.
当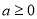 时
时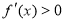 则
则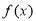 在
在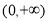 上是单调递增,
上是单调递增,
因此函数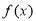 至多只有一个零点,不符合题意. 10分
至多只有一个零点,不符合题意. 10分
当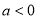 时,由
时,由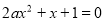 得
得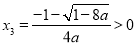
因此,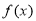 在
在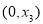 上是单调递增,在
上是单调递增,在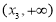 上是单调递减,
上是单调递减,
所以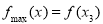 .
.
一方面,当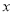 从右边趋近于0时,
从右边趋近于0时,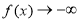 ;
;
当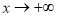 时,
时,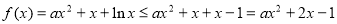
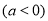
因此,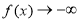 11分
11分
另一方面,由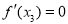 得
得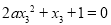 ,即
,即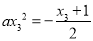
因此,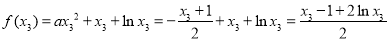
很明显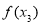 在
在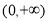 上是单调递增且
上是单调递增且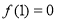
根据题意得 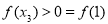 ,
,
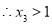 即方程
即方程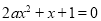 有且只有一个大于1的正实数根.
有且只有一个大于1的正实数根.
设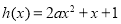 ,由
,由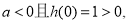 得
得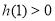 解得
解得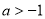
所以,实数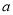 的取值范围是
的取值范围是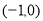 14分
14分
考点:应用导数研究函数的单调性、最值、函数的零点.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
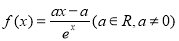 .
.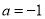 时,求函数
时,求函数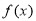 的极值;
的极值; 没有零点,求实数
没有零点,求实数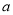 的取值范围.
的取值范围. ,则
,则 的是( )
的是( ) B.
B. C.
C. D.
D.
 在
在 上的图象是( )
上的图象是( )
 ,
, ,若
,若 ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.
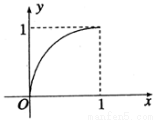
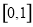 上的函数
上的函数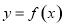 的图象如图所示,对于满足
的图象如图所示,对于满足 的任意
的任意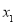 ,
,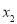 ,给出下列结论:
,给出下列结论: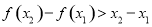 ;
;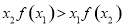 ;
;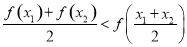 ;
;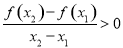 .
.
 的前
的前 项和为
项和为 ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 Z
Z 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数,则
上是单调增函数,则 的值为 .
的值为 .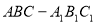 中,
中,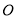 是
是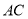 的中点,
的中点,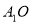 ⊥平面
⊥平面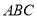 ,
, ,
,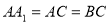 .
. 
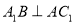 ;
;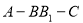 的余弦值.
的余弦值.