题目内容
求证:到圆心距离为a(a>0)的两个相离定圆的切线长相等的点的轨迹是直线。
答案:
解析:
解析:
| 证明:建立平面直角坐标系,设圆O以原点O为圆心,r为半径,圆A以点A(a,0)为圆心,半径为R。过点P(x,y)的直线PB与圆O相切于点B,直线PC与圆A相切于点C,且PB=PC
圆O的方程为x2+y2=r2 圆A的方程为(x-a)2+y2=R2 ∵PB=PC ∴PB2=PC2 由PO2-OB2=PA2-AC2 即x2+y2-r2=(x-a)2+y2-R2 得x= 这就是点P的轨迹方程,它表示一条垂直于x轴的直线。 |

练习册系列答案
相关题目

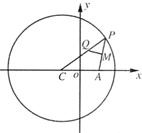 已知C为圆
已知C为圆 如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.
如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.