题目内容
 如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.
如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.(1)若∠PAB=30°,求以MN为直径的圆的方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内一定点.
分析:(1)根据题意可得圆O方程为x2+y2=4,直线l的方程为x=4.由∠PAB=30°算出直线AP、BP的方程,将x=4分别代入,可得M(4,2
)、N(4,-2
),由此即可算出以MN为直径的圆的方程;
(2)设点P的坐标为(x0,y0),由圆O的方程可得y02=4-x02.算出直线AP、BP以x0、y0为参数的方程,从而得到点M、N以x0、y0为参数的坐标,算出|MN|=
且MN的中点坐标为(4,-
).由此利用垂径定理加以计算,得到以MN为直径的圆截x轴的线段长为4
,从而可得该圆经过圆O内的定点C(4-2
,0).
| 3 |
| 3 |
(2)设点P的坐标为(x0,y0),由圆O的方程可得y02=4-x02.算出直线AP、BP以x0、y0为参数的方程,从而得到点M、N以x0、y0为参数的坐标,算出|MN|=
| 4|x0-4| |
| |y0| |
| 4(1-x0) |
| y0 |
| 3 |
| 3 |
解答:解:(1)∵圆O的圆心为原点O,直径|AB|=4,
∴圆O的半径r=2,可得圆O方程为x2+y2=4,
∵定直线l垂直于x轴正半轴,且到圆心O的距离为4,∴直线l的方程为x=4,
由∠PAB=30°,可得直线AP的斜率k=tan30°=
,所以直线AP的方程为y=
(x+2),
∵AB是圆O的直径,
∴AP⊥BP,可得直线BP的斜率k'=
=-
,直线BP的方程为y=-
(x-2).
将x=4分别代入直线AP、BP方程,可得M(4,2
)、N(4,-2
).
∴MN的中点坐标为(4,0),且MN=4
.
∴以MN为直径的圆,圆心为(2,0),半径R=2
,可得它的方程为(x-4)2+y2=12.
(2)设点P的坐标为(x0,y0),则x02+y02=4 (y0≠0),可得y02=4-x02,
∵直线AP的方程为y=
(x+2),直线BP的方程为y=
(x-2),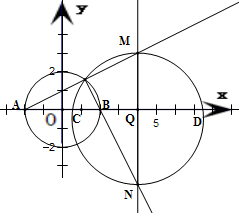
将x=4代入,可得M的纵坐标yM=
,N的纵坐标yN=
.
∴M(4,
)、N(4,
),
可得|MN|=|
-
|=
,
且MN的中点坐标为(4,-
).
由此可得以MN为直径的圆,圆心为(4,-
),
半径等于
,
由垂径定理,可得此圆截x轴的线段长度为:
|CD|=2
=
•
=
•
=4
(定值).
又∵直线MN经过x轴上的定点Q(4,0),Q为线段CD的中点,
∴以MN为直径的圆必过圆O内的定点C(4-2
,0).
∴圆O的半径r=2,可得圆O方程为x2+y2=4,
∵定直线l垂直于x轴正半轴,且到圆心O的距离为4,∴直线l的方程为x=4,
由∠PAB=30°,可得直线AP的斜率k=tan30°=
| ||
| 3 |
| ||
| 3 |
∵AB是圆O的直径,
∴AP⊥BP,可得直线BP的斜率k'=
| -1 |
| k |
| 3 |
| 3 |
将x=4分别代入直线AP、BP方程,可得M(4,2
| 3 |
| 3 |
∴MN的中点坐标为(4,0),且MN=4
| 3 |
∴以MN为直径的圆,圆心为(2,0),半径R=2
| 3 |
(2)设点P的坐标为(x0,y0),则x02+y02=4 (y0≠0),可得y02=4-x02,
∵直线AP的方程为y=
| y0 |
| x0+2 |
| y0 |
| x0-2 |

将x=4代入,可得M的纵坐标yM=
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
∴M(4,
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
可得|MN|=|
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| 4|x0-4| |
| |y0| |
且MN的中点坐标为(4,-
| 4(1-x0) |
| y0 |
由此可得以MN为直径的圆,圆心为(4,-
| 4(1-x0) |
| y0 |
半径等于
| 2|x0-4| |
| |y0| |
由垂径定理,可得此圆截x轴的线段长度为:
|CD|=2
|
| 4 |
| |y0| |
| 12-3x02 |
4
| ||
| |y0| |
| 4-x02 |
| 3 |
又∵直线MN经过x轴上的定点Q(4,0),Q为线段CD的中点,
∴以MN为直径的圆必过圆O内的定点C(4-2
| 3 |
点评:本题给出以原点为圆心的圆和直线l上的点M、N满足的条件,求以MN为直径的圆的方程及其性质.着重考查了求圆的标准方程、直线和圆的位置关系和点到直线的距离公式等知识,属于中档题.

练习册系列答案
相关题目
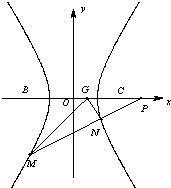 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.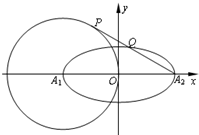 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆