题目内容
已知
，则函数y=sin4x-cos4x的最小值是________．
-1
分析：将函数y=sin4x-cos4x转化为y=-cos2x，利用余弦函数的性质即可求得其最小值．
解答：∵y=sin4x-cos4x
=（sin2x+cos2x）（sin2x-cos2x）
=-cos2x，
又x∈[-
，
]，
∴-
≤2x≤
，
∴-
≤cos2x≤1，
∴-1≤-cos2x≤．
∴函数y=sin4x-cos4x的最小值是-1．
故答案为：-1．
点评：本题考查二倍角的余弦与余弦函数的单调性与最值，属于中档题．
分析：将函数y=sin4x-cos4x转化为y=-cos2x，利用余弦函数的性质即可求得其最小值．
解答：∵y=sin4x-cos4x
=（sin2x+cos2x）（sin2x-cos2x）
=-cos2x，
又x∈[-
，]，∴-
≤2x≤，∴-
≤cos2x≤1，∴-1≤-cos2x≤
．∴函数y=sin4x-cos4x的最小值是-1．
故答案为：-1．
点评：本题考查二倍角的余弦与余弦函数的单调性与最值，属于中档题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
函数f（x）=Asin（ωx+φ）（其中
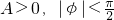）的图象如图所示，为了得到g（x）=sin2x的图象，则只需将f（x）的图象
，则关于x的方程f2（x）+bf（x）+c=0有7个不同实数解的充要条件是 
