题目内容
已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=
cos(
x)+log
x,则函数f(x)的零点有 个.
| 5 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
考点:函数的零点
专题:计算题,作图题,函数的性质及应用
分析:作f(x)=
cos(
x)+log
x(x>0)的图象,由图象解交点的个数,从而求零点的个数.
| 5 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
解答:
解:作f(x)=
cos(
x)+log
x(x>0)的图象如下图,

其在(0,+∞)上有三个零点,
又∵函数f(x)是定义在R上的奇函数,
∴函数f(x)的零点共有3×2+1=7个,
故答案为:7.
| 5 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |

其在(0,+∞)上有三个零点,
又∵函数f(x)是定义在R上的奇函数,
∴函数f(x)的零点共有3×2+1=7个,
故答案为:7.
点评:本题考查了函数的零点个数的判断,同时考查了数形结合的数学思想,属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
以茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )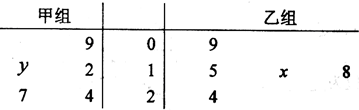

| A、5,2 | B、5,5 |
| C、8,5 | D、8,8 |


 如图,设A为半径为1圆周上一定点,在圆周上等可能的任取一点B,则弦长|AB|超过
如图,设A为半径为1圆周上一定点,在圆周上等可能的任取一点B,则弦长|AB|超过