题目内容
(本小题满分12分) 已知各项均为正数的数列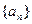 满足:
满足: 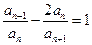 (
(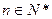 ),且
),且
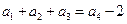 .
.
(Ⅰ)求数列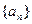 的通项公式;
的通项公式;
( Ⅱ)证明:
Ⅱ)证明: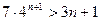 (
(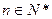 )
)
(Ⅲ)若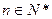 ,令
,令 ,设数列
,设数列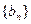 的前
的前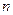 项和为
项和为 (
(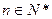 ),试比较
),试比较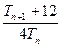 与
与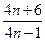 的大小.
的大小.
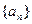 满足:
满足: 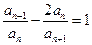 (
(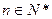 ),且
),且
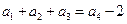 .
.(Ⅰ)求数列
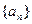 的通项公式;
的通项公式;(
 Ⅱ)证明:
Ⅱ)证明: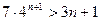 (
(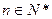 )
)(Ⅲ)若
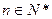 ,令
,令 ,设数列
,设数列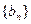 的前
的前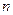 项和为
项和为 (
(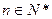 ),试比较
),试比较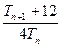 与
与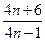 的大小.
的大小.(1)略
(2)
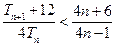
.解:(Ⅰ)∵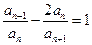 ,
,
(法一
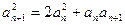 ,即
,即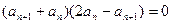
又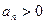 ,所以有
,所以有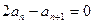 ,所以
,所以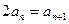 ,法二 令
,法二 令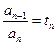
则有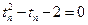 ,可得
,可得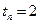 )
)
∴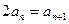 所以数列
所以数列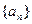 是公比为2的等比数列 (2分)
是公比为2的等比数列 (2分)
由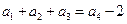
 得
得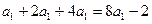 ,
, 解得
解得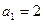
故数列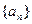 的通项公式为
的通项公式为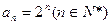 (4分)
(4分)
(Ⅱ)①当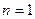 时,
时,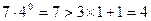 ,上面不等式显然成立;(5分)
,上面不等式显然成立;(5分)
②假设当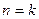 时,不等式
时,不等式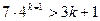 成立
成立
当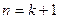 时,
时,
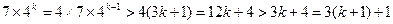
综上①②对任意的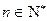 均有
均有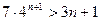 (8分)
(8分)
(Ⅲ)因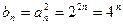 ,所以
,所以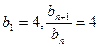
即数列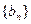 是首项为4,公比是4的等比数列 (9分)
是首项为4,公比是4的等比数列 (9分)
所以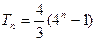 ,
,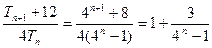 (10分)
(10分)
又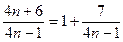 ∴
∴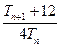 -
-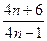 =
=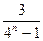 -
-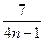
=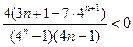
所以对任意的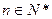 均有
均有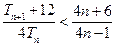 (12分)
(12分)
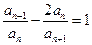 ,
,(法一

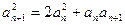 ,即
,即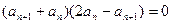
又
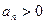 ,所以有
,所以有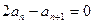 ,所以
,所以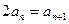 ,法二 令
,法二 令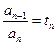
则有
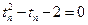 ,可得
,可得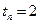 )
)∴
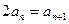 所以数列
所以数列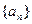 是公比为2的等比数列 (2分)
是公比为2的等比数列 (2分)由
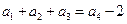
 得
得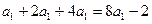 ,
, 解得
解得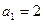
故数列
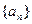 的通项公式为
的通项公式为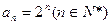 (4分)
(4分)(Ⅱ)①当
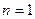 时,
时,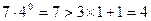 ,上面不等式显然成立;(5分)
,上面不等式显然成立;(5分)②假设当
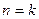 时,不等式
时,不等式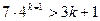 成立
成立当
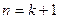 时,
时,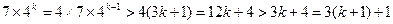
综上①②对任意的
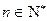 均有
均有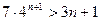 (8分)
(8分)(Ⅲ)因
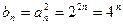 ,所以
,所以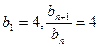
即数列
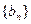 是首项为4,公比是4的等比数列 (9分)
是首项为4,公比是4的等比数列 (9分)所以
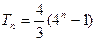 ,
,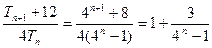 (10分)
(10分)又
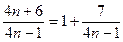 ∴
∴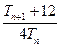 -
-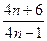 =
=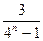 -
-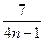
=
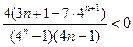
所以对任意的
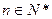 均有
均有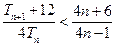 (12分)
(12分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
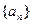 的前
的前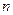 项和为
项和为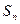 ,点
,点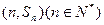 均在函数
均在函数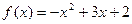 的图象上
的图象上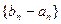 是首项为1,公比为
是首项为1,公比为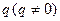 的等比数列,求数列
的等比数列,求数列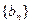 的前
的前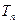 .
.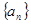 的前n项和为
的前n项和为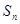 ,若
,若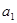 =11,且
=11,且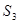 =27,则当
=27,则当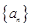 的前n项和为
的前n项和为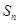 ,已知
,已知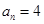 ,
,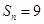 ,则
,则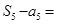 ( )
( ) 前n项和Sn;
前n项和Sn;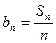 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.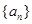 的前20项的和为100,那么
的前20项的和为100,那么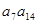 的最大值为
的最大值为 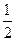 ,
,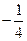 ,
,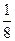 ,…的第8项是 .
,…的第8项是 .