Question

14．已知定义在R上的二次函数y=f（x）的图象开口向上且对称轴是y轴，求满足不等式f（a）＞f（3）的实数a的取值范围．

Answer 1

分析 根据题意，画出函数f（x）的大致图象，根据函数y=f（x）的图象与性质，讨论x＞0与x＜0时，f（x）的单调性，求出f（a）＜f（3）的解集即可．

解答 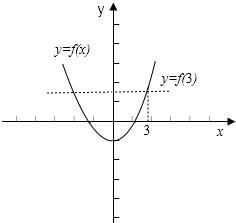解：根据题意，画出函数f（x）的图象，如图所示；
∵函数y=f（x）的图象是抛物线，开口向上且对称轴是y轴，
∴x＞0时，f（x）是单调增函数，满足f（a）＞f（3）的条件是a＞3；
x＜0时，f（x）是单调增函数，满足f（a）＜f（3）的条件是a＜-3；
综上，满足不等式f（a）＞f（3）的实数a的取值范围是：
{a|a＜-3或a＞3}．

点评 本题考查了二次函数的图象与性质的应用问题，也考查了数形结合的应用问题，是基础题目．