题目内容
(本小题满分12分)
已知函数 定义域为
定义域为 ,若对于任意的
,若对于任意的 ,都有
,都有 ,且
,且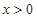 时,有
时,有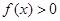 .
.
(1)求证:  为奇函数;
为奇函数;
(2)求证:  在
在 上为单调递增函数;
上为单调递增函数;
(3)设 ,若
,若 <
< ,对所有
,对所有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)见解析(2)见解析(3)
解析试题分析:(1)因为有 ,
,
令 ,得
,得 ,所以
,所以 , ……1分
, ……1分
令 可得:
可得:
所以 ,所以
,所以 为奇函数. ……4分
为奇函数. ……4分
(2) 是定义在
是定义在 上的奇函数,由题意
上的奇函数,由题意 则
则 ,
,
 是在
是在 上为单调递增函数; ……8分
上为单调递增函数; ……8分
(3)因为 在
在 上为单调递增函数,
上为单调递增函数,
所以 在
在 上的最大值为
上的最大值为 , ……9分
, ……9分
所以要使 <
< ,对所有
,对所有 恒成立,
恒成立,
只要 >1,即
>1,即 >0, ……10分
>0, ……10分
令

 . ……12分
. ……12分
考点:本小题主要考查有关抽象函数的奇偶性、单调性和恒成立问题,考查学生分析问题、解决问题和灵活转化的能力.
点评:解决抽象函数问题常用的方法是“赋值法”,而要考查抽象函数的性质,还要借助图象,数形结合来解决.对于恒成立问题,要转为为求最值来解决,而(3)中将函数转化为关于 的函数,是这道题解题的亮点所在.
的函数,是这道题解题的亮点所在.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
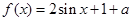 是一个奇函数.
是一个奇函数.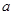 的值和
的值和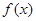 的值域;
的值域;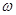 >
> ,若
,若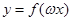 在区间
在区间 是增函数,求
是增函数,求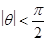 ,若对
,若对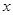 取一切实数,不等式
取一切实数,不等式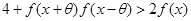 都成立,求
都成立,求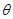 的取值范围.
的取值范围.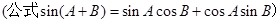
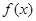 在定义域上是奇函数,且在
在定义域上是奇函数,且在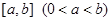 上是减函数,图像如图所示.
上是减函数,图像如图所示.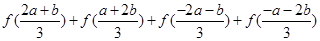 ;
; 上的图像;
上的图像;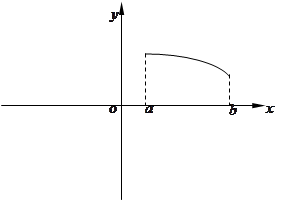
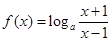 (
(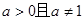 ).
).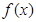 的奇偶性,并证明;
的奇偶性,并证明;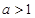 ,用单调性定义证明函数
,用单调性定义证明函数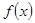 在区间
在区间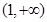 上单调递减;
上单调递减; ,使得
,使得 时,值域为
时,值域为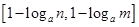 ,若存在,求出实数
,若存在,求出实数 为奇函数;
为奇函数; 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.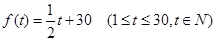 ,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).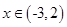 ,求函数
,求函数 =
=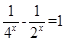 的最大值与最小值.
的最大值与最小值.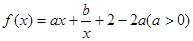 的图像在点
的图像在点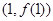 处的切线与直线
处的切线与直线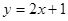 平行.
平行.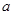 ,
,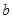 满足的关系式;
满足的关系式;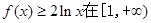 上恒成立,求
上恒成立,求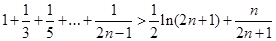 (
(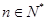 )
) .
.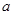 为何实数
为何实数 总是为增函数;
总是为增函数;