题目内容
(本题14分)
已知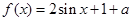 是一个奇函数.
是一个奇函数.
(1)求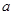 的值和
的值和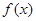 的值域;
的值域;
(2)设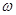 >
> ,若
,若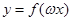 在区间
在区间 是增函数,求
是增函数,求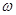 的取值范围
的取值范围
(3) 设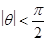 ,若对
,若对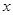 取一切实数,不等式
取一切实数,不等式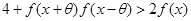 都成立,求
都成立,求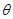 的取值范围.
的取值范围.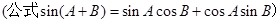
(1)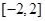 .(2)
.(2)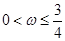 ;(3)
;(3) 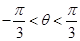 .
.
解析试题分析:(1)根据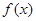 为奇函数,可得
为奇函数,可得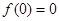 ,求得
,求得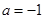 ,进而求解值域。
,进而求解值域。
(2) 首先把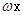 视为一个整体,求得得到函数的增区间,再利用
视为一个整体,求得得到函数的增区间,再利用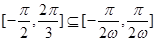
求得k值,进一步得到w的范围。
(3) 应用三角公式,将f(x)化简后, 得到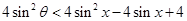 ,只需
,只需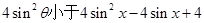 的最小值,转化成求二次函数的最小值问题。
的最小值,转化成求二次函数的最小值问题。
解:(1) 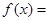
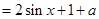 .
.
∵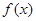 为奇函数,∴
为奇函数,∴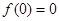 ,
, ,
,
∴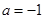 ,
,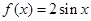 的值域为
的值域为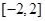 .
.
(2) 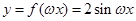 当
当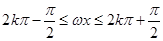 时,
时,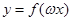 为增函数,∵
为增函数,∵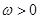
∴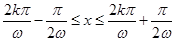 .
.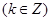 ,
,
∴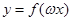 在区间
在区间 上是增函数
上是增函数
依题意得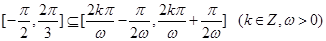 ,
,
∴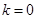 ∴
∴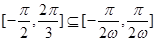 (
( ),
),
∴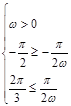 得
得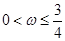 (也可根据图象求解).
(也可根据图象求解).
(3) 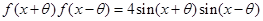
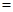
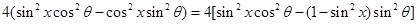
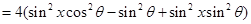
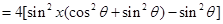
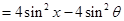 .
.
由原不等式得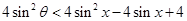
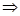
 ,
,
又∵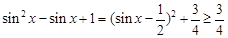 .当且仅当
.当且仅当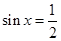 取等号.
取等号.
要使原不等式恒成立,须且只需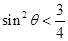 ,∴
,∴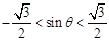 ,
,
∵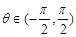 ,∴
,∴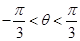 .
.
考点:本题主要考查函数单调性和奇偶性以及不等式的恒成立问题的运用。
点评:解决该试题的关键是利用函数为奇函数,得到参数a的值,进而分析函数的单调性,熟练的掌握三角函数的单调区间很重要。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
(本小题满分12分)探究函数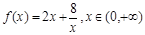 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数
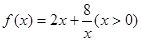 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数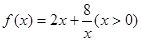 在区间 上递增.当
在区间 上递增.当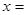 时,
时,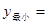 .
.(2)证明:函数
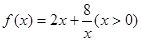 在区间(0,2)递减.
在区间(0,2)递减.(3)思考:函数
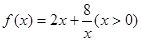 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明) 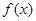 是定义在[-1,1]上的奇函数,当
是定义在[-1,1]上的奇函数,当 ,且
,且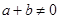 时有
时有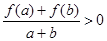 .
.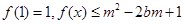 对所有
对所有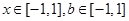 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 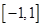 上的偶函数
上的偶函数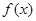 ,已知当
,已知当 时的解析式
时的解析式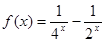
 在
在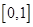 上的解析式;
上的解析式; 的最小值为1,且
的最小值为1,且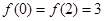 .
.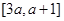 上不单调,求实数
上不单调,求实数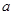 的取值范围;
的取值范围;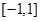 上,
上,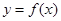 的图象恒在
的图象恒在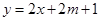 的图象上方,试确定实数
的图象上方,试确定实数 的取值范围.
的取值范围. 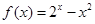 ,问方程
,问方程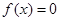 在区间[-1,0]内是否有
在区间[-1,0]内是否有 在(0,1)内恰有一解,求实数
在(0,1)内恰有一解,求实数 的取值范围.
的取值范围.  =
=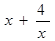
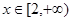 上是增函数;(2)求
上是增函数;(2)求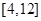 上的值域。
上的值域。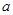 为非负实数,函数
为非负实数,函数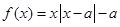 .
.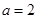 时,求函数的单调区间;
时,求函数的单调区间;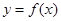 的零点个数.
的零点个数. 定义域为
定义域为 ,若对于任意的
,若对于任意的 ,都有
,都有 ,且
,且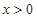 时,有
时,有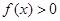 .
. ,若
,若 ,对所有
,对所有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.