题目内容
5.若函数f(x)=-2x3+ax2+1存在唯一的零点,则实数a的取值范围为( )| A. | [0,+∞) | B. | [0,3] | C. | (-3,0] | D. | (-3,+∞) |
分析 可化为a=2x-$\frac{1}{{x}^{2}}$,从而令g(x)=2x-$\frac{1}{{x}^{2}}$,求导g′(x)=2$\frac{(1+x)({x}^{2}-x+1)}{{x}^{3}}$,从而判断函数的单调性,从而作出其图象,利用数形结合求解.
解答 解:令f(x)=-2x3+ax2+1=0,
易知当x=0时上式不成立;
故a=$\frac{2{x}^{3}-1}{{x}^{2}}$=2x-$\frac{1}{{x}^{2}}$,
令g(x)=2x-$\frac{1}{{x}^{2}}$,则g′(x)=2+$\frac{2}{{x}^{3}}$=2$\frac{(1+x)({x}^{2}-x+1)}{{x}^{3}}$,
故g(x)在(-∞,-1)上是增函数,
在(-1,0)上是减函数,在(0,+∞)上是增函数;
故作g(x)=2x-$\frac{1}{{x}^{2}}$的图象如下,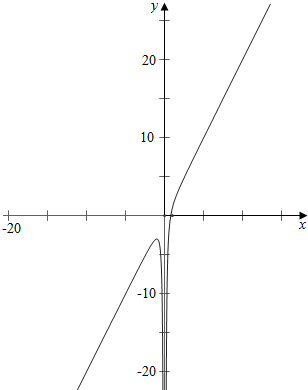 ,
,
g(-1)=-2-1=-3,
故结合图象可知,a>-3时,
方程a=2x-$\frac{1}{{x}^{2}}$有且只有一个解,
即函数f(x)=-2x3+ax2+1存在唯一的零点,
故选:D.
点评 本题考查了导数的综合应用及数形结合的思想应用,同时考查了函数的零点与方程的根的关系应用.

练习册系列答案
相关题目
20.如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是( )
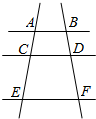

| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
 已知平面区域D由以P(1,2)、R(3,5)、Q(-3,4)为顶点的三角形内部和边界组成.
已知平面区域D由以P(1,2)、R(3,5)、Q(-3,4)为顶点的三角形内部和边界组成.