题目内容
已知定圆
圆心为A，动圆M过点B(1,0)且和圆A相切，动圆的圆心M的轨迹记为C.
（I）求曲线C的方程；
（II）若点
为曲线C上一点，求证：直线
与曲线C有且只有一个交点.
（Ⅰ）曲线C的方程为
（Ⅱ）见解析
解析:
（I）圆A的圆心为
，
设动圆M的圆心
由|AB|=2，可知点B在圆A内，从而圆M内切于圆A，
故|MA|=r1—r2，即|MA|+|MB|=4，
所以，点M的轨迹是以A，B为焦点的椭圆，
设椭圆方程为
，由
故曲线C的方程为 …………6分
（II）当
，
消去
①
由点为曲线C上一点，
于是方程①可以化简为
解得
，
综上，直线l与曲线C有且只有一个交点，且交点为.
练习册系列答案
步步高达标卷系列答案
相关题目
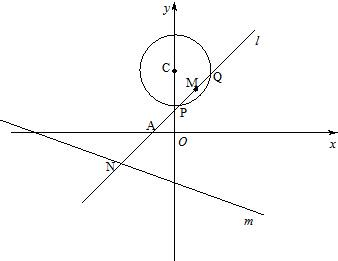如图，已知定圆C：x2+（y-3）2=4，定直线m：x+3y+6=0，过A（-1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，M是PQ中点．
圆心为A，动圆M过点B(1,0)且和圆A相切，动圆的圆心M的轨迹记为C.
为曲线C上一点，求证：直线
与曲线C有且只有一个交点.
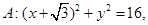圆心为A；动圆M过点
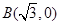且与圆A相切，圆心M 的坐标为
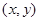且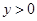
，它的轨迹记为C。
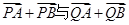互相垂直？若存在，求出点P，Q的横坐标，若不存在，请说明理由。