题目内容
如图,已知正方体ABCD-A1B1C1D1,E、F分别是平面A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( ).
| A.60° | B.45° | C.30° | D.90° |
B
解析试题分析:本题利用空间向量来求异面直线所成角,首先建立以D为原点的坐标系,进而写出两直线的方向向量,求两方向向量的夹角,从而确定直线所成角
考点:异面直线所成角
点评:向量在解决立体几何问题时将大量的思维代之以数据计算

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知正四棱柱 中,
中, ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )
A. | B. | C. | D. |
已知直线 、
、 、
、 不重合,平面
不重合,平面 、
、 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若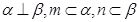 ,则 ,则 |
D.若 ,则 ,则 |
在正方体ABCD—A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( ) 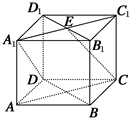
| A.AC | B.BD | C.A1D | D.A1D |
设 是平面
是平面 内的两条不同直线,
内的两条不同直线, 是平面
是平面 内两条相交直线,则
内两条相交直线,则 的一个充分不必要条件是( )
的一个充分不必要条件是( )
A. | B. |
C. | D. |
已知直线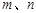 与平面
与平面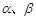 ,给出下列三个命题:
,给出下列三个命题:
①若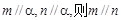 ②若
②若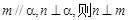
③若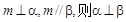 ④
④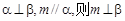
其中真命题的是( )
| A.②③ | B.②③④ | C.②③④ | D.①④ |
( )已知两个不同的平面 、
、 ,能判定
,能判定 //
// 的条件是
的条件是
A. 、 、 分别平行于直线 分别平行于直线 | B. 、 、 分别垂直于直线 分别垂直于直线 |
C. 、 、 分别垂直于平面 分别垂直于平面 | D. 内有两条直线分别平行于 内有两条直线分别平行于 |
用 、
、 、
、 表示三条不同的直线,
表示三条不同的直线, 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;②若
;②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;
;
③若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;④若
;④若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ;则其中正确的是( )
;则其中正确的是( )
| A.①② | B.②③ | C.①④ | D.③④ |
 =
= =
= ,则( )
,则( )