题目内容
如图,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且 =
= =
= ,则( )
,则( )
A.EF与GH互相平行
B.EF与GH异面
C.EF与GH的交点M可能在直线AC上,也可能不在直线AC上
D.EF与GH的交点M一定在直线AC上
D
解析试题分析:因为由 =
= =
= 可知在三角形CBD中,FG//BD,同理由于点E、H分别是边AB、AD的中点,那么说明FH//BD,但是平行不相等,因此是梯形,故E、F、G、H四点共面,同时设EH,FG延长且交与点P,那么利用AC是平面ABC,与平面ADC的交线,由于点P在EH上,点P在FG上,那么故可知由公理3可知点P 在交线AC上,故选D.
可知在三角形CBD中,FG//BD,同理由于点E、H分别是边AB、AD的中点,那么说明FH//BD,但是平行不相等,因此是梯形,故E、F、G、H四点共面,同时设EH,FG延长且交与点P,那么利用AC是平面ABC,与平面ADC的交线,由于点P在EH上,点P在FG上,那么故可知由公理3可知点P 在交线AC上,故选D.
考点:本题主要考查了四点是否共面的问题的运用。
点评:解决该试题的关键是利用相似比得到平行,同时利用平行的传递性得到,线线平行,确定出共面。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知三条直线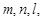 三个平面
三个平面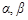 ,r,下列四个命题中正确的是( )
,r,下列四个命题中正确的是( )
A.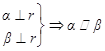 | B.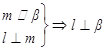 |
C. | D.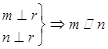 |
如图,已知正方体ABCD-A1B1C1D1,E、F分别是平面A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( ).
| A.60° | B.45° | C.30° | D.90° |
直线a、b、c及平面α、β,下列命题正确的是( )
A.若a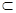 α,b α,b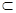 α,c⊥a, c⊥b 则c⊥α α,c⊥a, c⊥b 则c⊥α | B.若b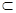 α, a//b则 a//α α, a//b则 a//α |
| C.若a//α,α∩β=b则a//b | D.若a⊥α, b⊥α 则a//b |
已知二面角 是直二面角,P为棱AB上一点,PQ、PR分别在平面
是直二面角,P为棱AB上一点,PQ、PR分别在平面 、
、 内,且
内,且 ,则
,则 为( )
为( )
| A.45° | B.60° | C.120° | D.150° |
已知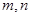 是两条不重合的直线,
是两条不重合的直线,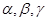 是三个两两不重合的平面, 给出下列四个命题:
是三个两两不重合的平面, 给出下列四个命题:
①若 ; ②若
; ②若 ;
;
③若 ;
;
④若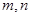 是异面直线,
是异面直线,
其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
若 是空间四条直线.如果“
是空间四条直线.如果“ ”,则( )
”,则( )
A. 且 且 | B. 中任意两条可能都不平行 中任意两条可能都不平行 |
C. 或 或  | D. 中至少有一对直线互相平行 中至少有一对直线互相平行 |
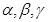 为两两不重合的平面,
为两两不重合的平面,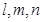 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: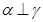 ,
,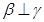 ,则
,则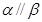 ;②若
;②若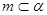 ,
,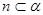 ,
,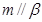 ,
,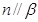 ,则
,则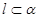 ,则
,则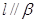 ; ④若
; ④若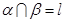 ,
,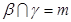 ,
,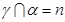 ,
,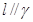 ,则
,则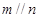 .其中真命题的个数是
.其中真命题的个数是  ,且PA,PB,PC两两垂直,则P到面ABC的距离为( )
,且PA,PB,PC两两垂直,则P到面ABC的距离为( )
