��Ŀ����
4��ij��ʳ��־�����ٰ�һ���ϱ���˵����ֻᣬ������60��һ�߳�ʦ����ʳר�Ҳμӣ���ͬ��ϵ�ij�ʦ����ʳר���������±���ʾ��| ��ϵ | ���� | ���� | ³�� | ������ |
| ���� | 20 | 15 | 15 | 10 |
��2�����������봨��������������ϵ��������������봨�˵ij�ʦ����ʳר����ѡ��2�����ԣ�������ר�ҷ�������ΪX�����������X�ķֲ��к���ѧ������
���� ��1������60����ʦ����ʳר�������ѡ��2��������������¼������������2������ͬһ��ϵ�����Ļ����¼��������ɴ������2������ͬһ��ϵ�ĸţ�
��2������������봨�˵ij�ʦ����ʳר����ѡ��2�����ԣ�������ר�ҷ�������ΪX����X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��� �⣺��1������60����ʦ����ʳר�������ѡ��2����
�����¼�����n=${C}_{60}^{2}$=1770��
2������ͬһ��ϵ�����Ļ����¼�����n=${C}_{20}^{2}+{C}_{15}^{2}+{C}_{15}^{2}+{C}_{10}^{2}$=445��
��2������ͬһ��ϵ�ĸ���p=$\frac{m}{n}$=$\frac{445}{1770}$=$\frac{89}{354}$��
��2������������봨�˵ij�ʦ����ʳר����ѡ��2�����ԣ�
������ר�ҷ�������ΪX����X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=$\frac{{C}_{15}^{2}}{{C}_{35}^{2}}$=$\frac{105}{595}$��
P��X=1��=$\frac{{C}_{20}^{1}{C}_{15}^{1}}{{C}_{35}^{2}}$=$\frac{300}{595}$��
P��X=2��=$\frac{{C}_{20}^{2}}{{C}_{35}^{2}}$=$\frac{190}{595}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{105}{595}$ | $\frac{300}{595}$ | $\frac{190}{595}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�

| A�� | 5x+4y-11=0 | B�� | 5x-4y-21=0 | C�� | 25x+16y-89=0 | D�� | 25x-16y-89=0 |
| A�� | ��0��3] | B�� | [$\frac{1}{3}$��3] | C�� | [$\frac{1}{3}$��3�� | D�� | [$\frac{1}{3}$��+�ޣ� |
| A�� | 2+$\sqrt{3}$ | B�� | 1+$\sqrt{3}$ | C�� | 3+$\sqrt{3}$ | D�� | $\sqrt{3}$ |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
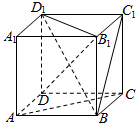 ����ͼ��ʾ��������ABCD-A1B1C1D1�У�
����ͼ��ʾ��������ABCD-A1B1C1D1�У�